KOLCHANOV N.A., MATUSHKIN Yu.G., FROLOV A.S.
Institute of Cytology and Genetics, (Siberian Branch of the Russian Academy of Sciences), 10 Lavrentieva ave., Novosibirsk, 630090 Russia
Keywords: regulaton mechanisms, hierarchical level, conformational stability
Regularities of evolutionary processes are being investigated theoretically basing on mathematical approaches from the moment the mathematical population genetics appeared. The complexity of biological objects lies in their multicomponent nature and occurrence of multiple regulatory feedbacks, which are interconnected through a variety of functional relations. The multiple regulatory circuits is a basically important feature that provide for the regulation of all functions of the organism.
Despite the diversity of regulatory circuits, they can be classified according to their hierarchical level in the regulation of vital activities of the organism. Regulatory circuits responsible for the function of individual genes or gene sets corresponds to the lowest regulatory level. Next are the circuits underlying the functions of cells, tissues, organs, and entire organisms. Endocrine and nervous systems are the regulatory circuits of the highest hierarchical level.
Biological systems contain two types of regulatory circuits: positive and negative feedbacks. The negative feedback is employed for maintenance of a parameter X under control within a narrow range around the level X0 that is optimal under certain environmental conditions. The value of the parameter X is recorded by the reception system and conveyed to the regulation module via the information channel. Flows of metabolites, hormones, mediators, neural impulses, etc., are used as information channels.
The function of the positive feedback is in the maximally efficient deviation of the parameter X from its initial value X0 after certain conditions were reached. Positive feedbacks provide for fast autoexcitation of elements of endocrine and nervous systems (important, in particular, in stress responses) as well as play the key role in regulation of morphogenesis, growth, and development of organs, the processes that in their essence is a rapid escape from the initial state.
Note also that the deviation of the value of the controlled parameter X from its optimal level X0 can result not only from the changes in internal and external environments but also from mutations; therefore, being the consequence of constantly occurring disturbances in cell genetic machinery. As it was mentioned earlier [1, 2], the nature of X fluctuations, internal or external, is nonessential for the function of negative feedback circuit.
Taking this into account, we considered a simplified model system applied to the cellular level of biological organisms [1, 2]; in this system, the concentration of the protein X in the organism is determined by two processes: its biosynthesis and degradation.
The mutations that altered the conformational stability of the protein and, consequently, its degradation rate, are the excitation agents that deviate the protein concentration from the optimal level X0. It is known that the decrease in conformational stability of a mutant protein causes the increase in its degradation rate, since the proteins with decreased stability have a loose structure, easily denature, and are rapidly destroyed by proteases. The dependence of the protein degradation constant on its conformational stability E is the following: if the value of E is positive, degradation rate varies in inverse proportion to conformational stability; if E is negative, the rate is constant.
We studied the effect of mutations affecting the conformational stability of the protein on the protein concentration in the systems with and without negative feedback. It was suggested that the probability of an individual carrying a protein with stability alteration 
to appear in the population followed a normal distribution:
 |
(1) |
where 
is the parameter characterizing the mutation frequency. Qualitatively, is describing the range of the originating genotypic variation. Distribution of the population frequency of the individuals with different concentrations of the mutant protein is a convenient characteristics to describe the range of the observed, that is, phenotypic, variation.
Population number Ne was constant. Reproduction of individuals was performed according to their fitness, which depended on the following equation and followed a normal distribution:
 |
(2) |
where X0 is the optimal protein concentration for this environment and 
is dispersion of permissible concentration alterations. Under conditions of stabilizing selection, the external environment is constant, and is reflected at every stage of modeling the optimal protein concentration. The closer is the protein concentration in a given individual to the optimal level, the higher is its fitness.
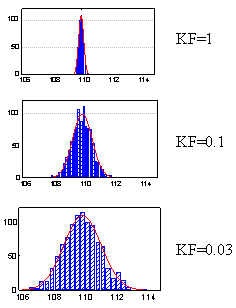
Mutation ranges calculated for the populations under the effect of different negative feedback force KF are shown in Fig. 1. The KF value equal to 1 represents a very strong negative feedback; KF = 0.1, intermediate; and KF = 0. 03, its absence.
A considerable variation of the protein concentration is typical of the populations of individuals lacking the negative feedback. However, the observed variation value is decreasing with the increase in the feedback force; this decrease manifests itself by narrowing of the variation range. Thus, the negative feedback minimizes the phenotypic manifestation of the mutations through the decrease in the protein concentration deviation from the normal level under mutational alterations of its conformational stability. In this case, it occurs through the increase in the protein biosynthesis rate if mutations increase the rate of its degradation and decrease in the protein biosynthesis rate if mutations decrease its degradation rate. Actually, and this conclusion is very important, any negative feedback minimizes (disguises) the phenotypic manifestation of mutation through compensatory alteration of the intensity of the regulated process.
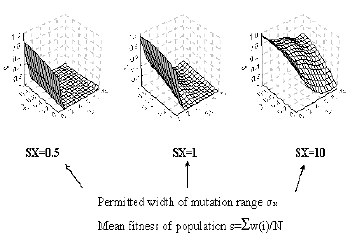
The dependence of the mean fitness of the population (S) upon two parameters, feedback force (KF) and mutation frequency (SE), is shown in Fig. 2. Note that at a fixed feedback force (KF), the increase in mutation frequency (SE) causes a gradual decrease in fitness. A limiting region of SE values exists, to the right of which the population fitness tends to zero (that is, the population dies). In terms of M. Eigen, this critical value may be named the boundary of mutational error catastrophe. The negative feedback under conditions of stabilizing selection can be considered an essential factor of population fitness. That is why the evolution of a population under the effect of stabilizing selection is directed toward the improving the negative feedbacks, that is, the population advances along the line of constant mutation frequency SE toward the increase in the feedback force.
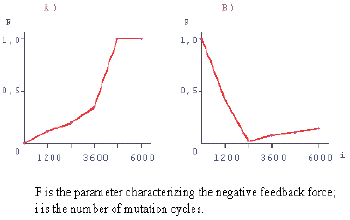
The changing in the negative feedback force (calculated from the results of modeling) in the course of stabilizing selection, the averaging of the force provided, is shown in Fig. 3. Under these conditions, a monotonic increase in the negative feedback force takes place, as the force reaches the stationary level. Thus, the stabilizing selection is a factor of evolutionary origination, maintenance, and improvement of negative feedbacks.
The evolution of the negative feedback under the effect of the directional selection, connected with monotonic alteration of environment, is completely different. In this case, the optimal concentration of protein X0, which determines the fitness, changes by the value 
at each step of the modeling. The value thus specified is actually determining the rate of environmental changes. The analysis performed has demonstrated that under conditions of a directional selection, those individuals that lack negative feedback display highest fitness, whereas the individuals with negative feedback are dislodged from the population. In this case, negative feedback hampers adaptation of individuals to new environment through maintaining the critical parameter X at a constant level X0, which now does not meet the changed environmental conditions.
Thus, we can state that a destruction (breakdown) of the negative feedback circuit occurs under conditions of the directional selection, which is a necessary condition for evolutionary adaptation of individuals to changing environmental conditions.
Hierarchical regulation is a typical feature of biological systems. To study the evolutionary peculiarities of biological systems with hierarchical regulation, we considered the model shown in Fig. 4. A parameter X regulated by negative feedback circuit corresponds to the highest hierarchical level. In turn, the parameter X is determining the value of a parameter Y that belongs to a lower hierarchical level. To make it more illustrative, suppose that the parameter X is a certain hormone or growth factor and its concentration determines the growth rate of a corresponding organ according to the equation 
Then the value of Y by the moment t is equal to 
, that is, depends exponentially on both the concentration of regulating factor and time of its action.
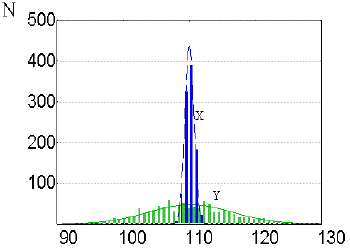
Now let’s employ this dependence to study the variation of the parameter Y when the parameter X is being mutationally changed. Comparison of the variation ranges of the parameters X and Y when the negative feedback controlling the parameter X is absent is shown in Fig. 5. Note that in this case, the variation of the parameter Y exceeds considerably the variation of the parameter X. Qualitatively, this situation is due to the fact that any mutational deviations of the parameter X from its normal value are exponentially amplified resulting in considerably larger deviations of the parameter Y. This effect can be described as a hypermanifestation of the Y variation range under the effect of mutation of a hierarchically higher parameter X.
Let’s consider the situation when the hierarchically higher parameter X is regulatory, while the fitness of the organism is determined by the value of parameter Y. If the negative feedback controlling X is lacking, the fitness of the population relative to the parameter Y is minimal. The reason is the hypermanifestation of the Y variation appearing in case the hierarchically higher parameter X mutates. However, the fitness of the population relative to the parameter Y increases with the increase in the force of the negative feedback controlling the parameter X (Fig. 6).
The negative effect of hypermanifestation can be suppressed when the originated regulatory circuit with negative feedback is powerful, that is, able to decrease the variation of the hierarchically higher parameter X maximally. Qualitatively, it means that ever growing limitation of variation of hierarchically high regulatory levels is required with the complication of the hierarchical organization of the organisms in order to keep their fitness constant.
In this connection, it is interesting to evaluate the mutation frequency at different hierarchical levels of regulation. We have carried out such evaluations for the genome of E. coli basing on our previous computer model that allowed us to calculate the frequency of repeat-based short deletions and duplications. The mutations based on repeats are known to contribute maximally to the variation of E. coli genome. We have analyzed the nucleotide sequences from various E. coli genomic regions that belong to two hierarchical levels: highest including such regulatory regions as promoters, operators, and replication starts, and lowest including gene coding regions. Note (Fig. 6) that the frequency of mutations in hierarchically high genomic regions is approximately by the order of magnitude higher than that in the gene coding regions, subordinate to them.
How can we reconcile this result to the above-described fact that a high variance of higher regulatory levels decreases drastically the organisms’ fitness? The problem is solved if we suggest that under conditions of stabilizing selection, high mutation frequency at higher regulatory levels is neutralized by negative feedback relations. In this case, as it was demonstrated above, a higher mutation frequency at high regulatory levels will not decrease the fitness. However, high mutation frequency of the regulatory regions provides considerable evolutionary advantages under changing environmental conditions. Under these conditions, a breakdown of regulatory circuits of negative feedback type and appearing of disguised variation of the highest regulatory level (parameter X) should not be expected. In turn, this should cause a hypermanifestation of Y variation (a lower regulatory level), which increases population fitness and enhances the search for new genotype variants able to adapt to the changing environment.
Thus, both the mechanism for increasing the accuracy of the systems possessing negative feedback and the ability of this mechanism to adapt to various environmental conditions are realized through the hierarchical system of regulation.
Our mathematical models allow the initial effect of destabilizing selection to be described qualitatively. This effect lies in destruction of regulatory circuits under systematically manifested and continuous changing of environmental conditions in one direction. In this case, an explosive increase in the rate and range of phenotypic variation, which previously was disguised by compensatory effects of regulatory circuits, is most likely. This increase will be the more pronounced, the higher hierarchical regulatory level is destroyed in the course of destabilizing selection.
Acknoledgements.
This work was supported by grants from the Russian Foundation for Basic Research (No.97-04-49740, 97-07-90309, 96-04-50006, 98-04-49479, 98-07-90126); Russian Ministry of Science and Technologies; Russian Human Genome Project; Russian Ministry of High Education; Siberian Department of RAS (Programm of Integration projects); National Institutes of Health, U.S.A. (No.5-R01-RR-04026-08).
References
- N.A .Kolchanov and H.A. Lim, “Computer analysis of genetic macromolecules. Structure, function and evolution.”(World Scientific Publishing, 1994).
- N.A. Kolchanov, and I.N. Shindyalov “Theoretical study of evolution of regulatory circuits”, In: “Problems of genetics and evolutionary theory” (V.K. Shumny and A.O. Ruvinsky, eds., Nauka, Sibirskoe Otdelenie, 1991).
|
|
|
| Fig. 1. Neutralization of mutation range under the effect of negative feedback |
Fig. 2. The effect of feedback force (KF) and mutation frequency (SE) on the mean fitness of population. |
|
|
|
| Fig. 3. Modeling of negative feedback evolutionary origination | Fig. 4. Simplest model of a hierarchically organized biological system |
 |
 |
| Fig. 5. Hypermanifestation of the variation range in a hierarchically organized biological system | Number of generations Fig. 6. Effect of the negative feedback controlling parameter X on the population fitness relative to parameter Y |
