A NEW METHOD OF SPECTRAL ANALYSIS OF DNA/RNA AND PROTEIN SEQUENCES

BAJIC V.B.+, BAJIC I.V.*, HIDE W.#

Centre for Engineering Research, Technikon Natal, P.O.Box 953, Durban 4000, South Africa; bajic.v@umfolozi.ntech.ac.za;

*Department of Electronic Engineering, University of Natal, Durban, South Africa; bajici@eng.und.ac.za;

#South African National Bioinformatics Institute (SANBI), South Africa; winhide@techno.sanbi.ac.za;

+Corresponding author

Keywords: spectral analysis, artificial neural networks, promoters, signal processing

 

A new methodology for the analysis of DNA/RNA and protein sequences is presented. It is based on a combined application of spectral analysis and artificial neural networks for extraction of common spectral characterization of a group of sequences that have the same or similar biological functions. The method does not rely on homology comparison and provides a novel insight into the inherent structural features of a functional group of biological sequences. The nature of the method allows possible applications to a number of relevant problems such as recognition of membership of a particular sequence to a specific functional group or localization of an unknown sequence of a specific functional group within a longer sequence. The results are of general nature and represent an attempt to introduce a new methodology to the field of biocomputing.

Note Due to the space limitation we will refer in this presentation only to a small number of references and thus inevitably make injustice to many important contributions in biocomputing field. We apologize to those authors whose references are omitted.

1. Introduction

One of the most exciting areas of research in science today is the decoding of information contained in DNA/RNA sequences. There are many approaches that attempt to deal with different aspects of this general problem. Some are based on homology between different sequences [1,2]. The other use different mathematical tools such as position weight matrix (PWM) [see 3,4], different statistical methods [5,6,7], hidden Markov models [8], generalized hidden Markov models [9], artificial neural networks (ANNs) [10,11,12,9], linguistic methods [13], decision trees [14], phylogenetic footprinting [15], dynamic programming [16,12], pattern recognition [17], etc., to mention few, as well as some of their combinations [see references in 18,9]. All these methods consider the genetic sequences as temporal patterns.

There have been other attempts to discover the informational content of genetic sequences, based on conversion of temporal genetic signal patterns by means of discrete Fourier transforms (DFT) or Fast Fourier transform (FFT) into different, the so called spectral domain, and then aimed for further analysis from that viewpoint. In the last 13 years such conceptually interesting methodology initially named the Information Spectrum Method (ISM) [19] and later, after further development, renamed to the Resonant Recognition Model (RRM) [20,21], has been developed. The method is aimed to find the spectral characterization, the so-called consensus spectrum (CS), of a group of sequences that have the same or similar type of biological functions. The basis of the method is the classical cross-spectral analysis. However this method, more precisely the part that relates to spectral analysis, unfortunately produces misleading results. In a recent publication [22] some very big discrepancies have been reported with regards to the published spectral characterization of specific biological sequences such as promoters. This motivated a detailed analysis of the source of error produced by the ISM (RRM) which is given in [23].

In this presentation we suggest an alternative methodology that we name SPANN (Signal Processing and ANN method) that is also based on signal processing concepts and additionally combined with the ANNs. This new methodology does not suffer deficiencies of the ISM (RRM) approach and opens up unique possibilities for examination of genetic sequences from a completely different viewpoint.

2. SPANN Method

The presentation of the SPANN method follows [23]. Analogously to ISM (RRM), SPANN treats biological sequences (DNA/RNA and proteins) as signals. DNA/RNA can be considered as sequences composed of only 4 different types of nucleotides, while proteins are considered as sequences composed of 20 different types of amino-acids. To convert these linear structures to a form suitable for application of signal processing, specific numbers are allocated to each of the nucleotides or each of the amino-acids. A typical technique for this is based on the so-called Electron-Ion Interaction Potential (EIIP) which correlates some physical characteristics of nucleotides and amino-acids and some biological properties of organic molecules [24]. These numerical values are precalculated and can be found in [20,21]. After assigning the relevant EIIP numbers to the elements of biological sequences they become simply numerical sequences. From this point on the extraction of the informational content of selected biologically related sequences is an engineering problem. Also, this is the point up to where the similarity between the ISM (RRM) and SPANN exists.

The description of the SPANN follows. Let us assume that is a set of numerical sequences obtained from a set of genetic sequences with a similar biological function. In general, sequences are of different lengths. All sequences are firstly detrended. A specific discrete domain transform, say DFT (but the other discrete transforms can also be used [23]), is applied to each of these detrended sequences and in this way their transform equivalents which form the set are obtained. From the relevant normalized power spectrum is formed making the set . The spectra in question may also be obtained as higher-order spectra that may be more useful in some cases [23]. These spectra are normalized with regard to domain transform variable (in the case of DFT this will be the frequency) as well as to overall power of the sequence. The cross-spectrum (CS) determination is different from the common approach used in signal processing. The CS of the whole set is obtained in the following way: the normalized domain variable interval is divided into N equal subintervals , where N is a selected positive integer. The normalised power pik contained in each of the in the k-th interval is calculated and their normalized product (product is made with regard to i) represents the k-th component in the ‘consensus’ power spectrum of the whole set . Then from all components in the CS we select those that we consider sufficiently significant. Let us denote the set of their indices by J. In the next phase an ANN is used and trained to recognise if the sequence examined belongs to the analysed functional set. The ANN training is based on the positions (determined by J) of the selected significant components in the individual spectra , as well as the amplitude of components.

If N = min(length() then the basic form of CS in SPANN is obtained. This is the form recommended. In this case the length of the shortest sequence in the examined set determines the resolution of CS. The CS obtained in this way represents a specific distribution of normalised power of signal over the normalised domain variable interval. However, this resolution may not always be sufficient to distinguish between subtle power distribution of longer sequences. Then we may need better resolution. If N > min(length() then the resolution of the CS is increased. However, this option has to be used with the extreme care as we may loose some of possibly important information contained in spectra of sequences whose length is larger than or equal to N. This happens if the spectral information is in the intervals  which do not contain active components of sequences with length less than N. So, this represent a kind of trade-off. In the pathological cases it may happen that the CS is empty due to the above-mentioned effect of vanishing cross-products. The analogous technology applies to higher-order cross spectra determination.

3. Is the SPANN method relevant for biocomputing ?

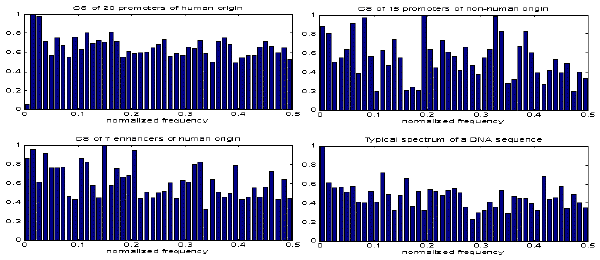
We present only some preliminary results to illustrate the relevance of SPANN methodology for biocomputing problems and to indicate possible domains of its applications. Let us consider if the spectral information of functionally related sequences has relevance in the context of recognising membership of a sequence to that specific functional group. We used sets of 28 promoters of human origin, 20 promoters of non-human origin and 16 other sequences of types different from these two mentioned. All sequences have been selected arbitrarily from GENBANK with the only criterion that their length is 87 or higher (the value of 87 has also been arbitrarily chosen). We applied SPANN methodology and produced, for illustration purposes, linear CS for promoters of human origin (Fig.1), promoters of non-human origin (Fig.2) and enhancers (Fig.3). A typical power spectrum determined according to SPANN for one of the promoters in the examined set is shown in Fig.4. It is evident that the power spectral distribution for a group of sequences shows differences from group to group (see Figs.1-3). This indicates that if sequences in the examined group are strongly functionally related, then the information in the group’s CS may be expected to strongly correlate to that common biological function of the sequences in the group. This is the basis on which the SPANN method relies.

 

Figs. 1-4 counted from left to right and top down

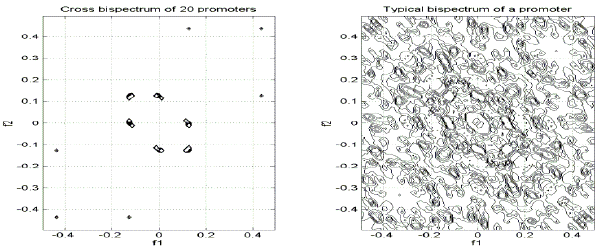
To illustrate the capabilities of SPANN with regard to the sequence recognition problem, the consensus bispectrum is determined for the group of 20 promoters of human origin. This bispectrum is shown in Fig.5. A typical bispectrum of a promoter from the examined group is shown in Fig.6. Consensus bispectra, like linear CS, may be considered as specific ‘spectral fingerprints’ of the examined group of functionally related sequences. They serve to make a selection of the relevant spectral components for the examined group of sequences.

Figs. 5-6 – consensus bispectrum and bispectrum

After selection of significant spectral components, an ANN has been trained to distinguish between the promoter and non-promoter sequences. The results are summarised in Table 1.

 

Table 1.

prom. (tr. set)

prom. hum.

prom. non-hum.

other

prom. (total)

No. of seq.

20

8

20

16

48

correct rec.

50% (10)

37.5% (3)

75% (15)

N/A

58.33% (28)

false posit.

N/A

N/A

N/A

12.5% (2)

N/A

 

The training set used is very small and selection of sequences from the public database is made without any aim to group them more precisely with regard to their function. However, although provisional, the results indicate that spectral characterisation of a group of sequences may have relevance in the sequence recognition problem. A rough comparison can be made with the overview results from [18] and implies that our preliminary results are comparable with those analysed in [18]. Possible application of SPANN is in sequence recognition and sequence location.

Conclusions

A new method for the analysis of genetic sequences was presented. It provides new insight into the information encoded in the DNA/RNA structures and opens up new ways of discovering the information hidden in genetic code.

References

  1. W. Gish and D.J. States, “Identification of protein coding regions by database similarity search”, Nature Genet. 3, 266-272 (1993)
  2. M.S. Gelfand, A.A. Mironov and P.A. Pevzner, “Gene recognition via spliced sequence alignment”, Proc.Nat.Acad.Sci. 93, 9061-9066 (1996)
  3. O.G. Berg and P.H. von Hippel, “Selection of DNA binding sites by regulatory proteins”, Trends Biochem. Sci. 13, 207-211 (1988)
  4. J.W. Ficket, “Quantitative discrimination of MEF2 sites”, Mol. Cell Bioll. 16, 437-441 (1996)
  5. P. Senapathy, M.B. Shapiro and N.L. Harris, “Splice junction, branch point sites and exons: sequence statistics, identification, and application to genome project”, Meth. Enzymol. 183, 252-278 (1990)
  6. A.E. Kel, M.P. Ponomarenko, et al., “SITEVIDEO: A computer systems for functional site analysis and recognition”, Comput. Applic. Biosci. 9, 617-627 (1993)
  7. M.P.Ponomarenko, A.N. Kolchanova and N.A. Kolchanov, “Generating programs for predicting the activity of functional sites”, J. Comput. Biol. 4, 83-90 (1997)
  8. A. Krogh, M. Brown, I.S. Mian, K. Sjolander and D. Haussler, “Hidden Markov models in computational biology: Application to protein modeling”, JMB, 235, 1501-1531, Feb. (1994)
  9. G. Reese, F.H. Eeckman, D. Kulp and D. Haussler, “Improved Splice Site Detection in Genie” J.Comp.Biol. 4, Issue 3, 311-323 (1997)
  10. E. Uberbacher and R. Mural, “Locating protein coding regions in human DNA sequences by a multiple sensor – neural network approach”, Proc. Nat. Acad. USA 88, 11261-11265 (1991)
  11. S.J. Brunak, J. Engelbrecht and S. Knudsen, “Prediction of human mRNA donor and acceptor sites from the DNA sequence”” J. Mol. Biol. 220, 49-65 (1991)
  12. E.E. Snyder and G.D. Stormo, “Identification of coding regions in genomic DNA sequences: an application of dynamic programming and neural networks”, Nucl. Acids Res. 21, 607-613 (1993)
  13. S. Dong and D.B. Searls, “Gene structure prediction by linguistic methods”, Genomics 162, 705-708 (1994)
  14. C. Burge and S. Karlin, “Prediction of complete gene structures in human genomic DNA”, J. Mol. Biol. 268, 79-94
  15. L. Duret and P. Bucher, “Searching for regulatory elements un human noncoding sequences”, Curr. Opin. Struc. Biol. 7, 399-406 (1997)
  16. M.S. Gelfand and M.A. Roytenberg, “Prediction of the exon-intron structure by a dynamic programming approach”, BioSystems 30, 173-182 (1993)
  17. Y. Xu and E. Uberbacher, “Gene prediction by pattern recognition and homology search”, ISMB-96, St. Louis, (AAAI Press) June (1996)
  18. J.W. Ficket and A.G. Hatzigeorgiou, “Eukaryotic Promoter Recognition”, Genome Res. 7, 861-878 (1997)
  19. V. Veljkovic, I. Cosic, B. Dimitrijevic and D. Lalovic, “Is It Possible to Analyze DNA and Protein Sequences by the Methods of Digital Signal Processing”, IEEE Trans. Biomed. Eng. BME-32, 337-341 (1985)
  20. I. Cosic, “Macromolecular Bioactivity: Is It Resonant Interaction Between Macromolecules ? – Theory and Applications”, IEEE Trans. Biomed. Eng. BME-41, 1101-1114 (1994)
  21. I. Cosic, “The Resonant Recognition Model of Macromolecular Bioactivity – Theory and Applications”, Birkhauser (1997)
  22. V.B. Bajic, I.V. Bajic and W. Hide, “Application of the RRM to a set of human promoters: A word of warning”, accepted SSCC98 (1998)
  23. V.B. Bajic and I.V. Bajic, “Spectral methods for analysis of DNA/RNA and protein sequences”, Technical Report, Technikon Natal, Durban, South Africa (1998)
  24. V. Veljkovic and I. Slavic, “General models of pseudo-potentials”, Phys. Rev. Lett. 29, 105-108 (1972)