RECOGNITION ACCURACY OF DNA FUNCTIONAL SITES CAN BE INCREASED BY AVERAGING PARTIAL RECOGNITIONS

PONOMARENKO M.P., FROLOV A.S., PONOMARENKO J.V., PODKOLODNAYA O.A., VOROBIEV D.G., KOLCHANOV N.A., OVERTON G.C.

Laboratory of Theoretical Genetics, Institute of Cytology and Genetics, Siberian Branch of the Russian Academy of Sciences, 10 Lavrentiev Ave., Novosibirsk, 630090, Russia, e-mail: pon@bionet.nsc.ru

GC Overton 105 111 Center for Bioinformatics, UPenn, Philadelphia, USA; e-mail: coverton@cbil.humgen.upenn.edu

Keywords: site recognition, activated database, central limit theorem, program generation

The Central Limit Theorem-based approach for increasing accuracy of the recognition of a functional site in an arbitrary DNA sequence has been suggested. It implies the averaging of a huge number of partial recognitions of the site into the “mean recognition” of this site. To generate a huge number of the partial recognition within the framework of the consensus and frequency matrix formalisms, a lot of novel oligonucleotide alphabets were used. On this basis, the activated database SAMPLES has been created. SAMPLES contains the sets of experimentally identified functional sites aligned and transformed into recognizing procedures. The SAMPLES applicability was tested using GATA-1 and C/EBP transcription factor binding sites. SAMPLES is available at http://wwwmgs.bionet.nsc.ru/.

Introduction

Recognition of functional sites in nucleotide sequences is one of the key episodes in genomic DNA annotation [1]. A huge number of methods have been so far developed to address the problem (for review, see [2]). The most widely used are the consensus and matrix methods [3-7] based on the evolutionary conservative nucleotides of functional sites. Recent evaluations of the accuracies of these methods for annotation of long genomic DNA fragments [8, 9] have demonstrated, on the one hand, a drastic progress in recognition of unknown genes and regulatory regions encoded in the genomic DNA and, on the other, the demand for considerable increase in the accuracy of the recognizing procedures for the functional sites in the actual application of genomic DNA annotation [8, 9].

Basing on the above bulk of intelligence, we are suggesting a systemic approach aiding the increase in the accuracy of a given functional site recognition in the course of genomic DNA annotation. It implies the averaging of a huge number of partial recognitions of the site analyzed into the “mean recognition” of this site. The consensuses and frequency matrixes in 20 novel computable alphabets have been used, and the activated database SAMPLES has been created. It contains experimentally identified DNA site sequences multiply aligned and transformed into the C-code recognition programs. The approach proposed was tested using GATA-1 and C/EBP transcription factor binding sites. SAMPLES is available at http://wwwmgs.bionet.nsc.ru/

System and methods

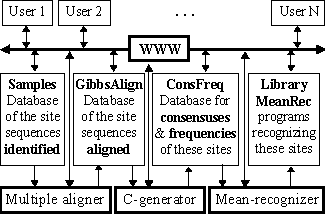
The scheme of the system suggested is shown in Fig.1. Its key module is the automated C-generator for the programs recognizing a functional site; the initial data for this recognition are the aligned sequences of this site DNA.

For the site consensus, the letters positioned with frequencies higher than the threshold f₀ are selected. Fig. 2 exemplifies the simplest C-code programs recognizing GATA-1 site by (a) its consensus and (b) its frequency matrix as well as (c and d) the simplest C-code programs generated for a huge number of consensuses and frequency matrices using the novel alphabets (Table 1). Using the database GibbsAlign of the multiply aligned site sequences (Fig. 1), SAMPLES generates all the consensuses and frequency matrices {f_k} recognizing this site in an arbitrary DNA (1? k? K). The simplest simultaneous usage of all the partial recognitions is averaging their values {f_k(S)} over the region S of a DNA sequence is the following:

(1)

where the recognition values f_k(S) are normalized as and the excision rule is: The Central Limit Theorem states that this mean recognition F_K should be Gaussian with the variation K^-1/2-reduced with the K increase.

Results and discussions

The mean recognition parameter suggested has been used to process the experimentally identified and aligned DNA sequences of GATA-1 and C/EBP transcription factor binding sites (the total number of the sequences analyzed was 102 and 62, respectively). All the data are available in the databases SAMPLES and GibbsAlign at http://wwwmgs.bionet.nsc.ru/ (Fig. 1). Each of these two sequence sets was randomly divided into non-overlapping 50%-subsets, training and control. In the training sets, all the possible consensuses and frequency matrices were generated. Their C-programs recognizing the sites are stored in the database ConsFreq and executable in the library MeanRec, http://wwwmgs.bionet.nsc.ru/ (Fig.1).

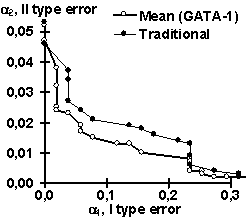
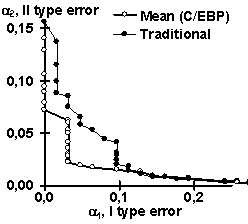
Using the control subsets and 1000 random DNA sequences, each of the partial recognition procedures was tested. These control results are listed in Table 2. Similarly, their mean recognitions have been tested (Table 2). Note that the partial recognitions differ from one another in their means and standard deviations as well as type I and II error rates of both the site and random DNA sequences. Essentially, it is impossible to predict what partial recognition would be the best for an arbitrary site; in contrast, the mean recognition appears the best for each of the three sites tested. Fig. 3 illustrates that the mean recognition can decrease both the type I and II errors, a₁ and a₂, with respect to the frequency matrix. This is shown for (a) GATA-1 and (b) C/EBP transcription factor binding sites.

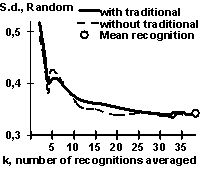
To study this, we analyzed the alteration of the statistical properties of the standard deviation of the GATA-1 mean recognition F_K with the growth of the total number K of the GATA-1 averaged partial recognition procedures. In this test, for each value K, ten different combinations of the partial recognition procedures {f_k} was randomly chosen and their standard deviations for 51 control sequences of the GATA-1 site and 1000 random DNA sequences were calculated and averaged. Two variants of this analysis were carried out: with and without the GATA-1 consensus and frequency matrix used traditionally for the GATA-1 recognition. The results obtained are presented in Fig. 4 for (a) the GATA-1 control subset and (b) for the random DNA (bold line, with traditional recognitions; broken line, without). In case of GATA-1 sites (Fig. 4a), the standard deviation value is approximately constant at any K value when the traditional recognitions are employed (Fig. 4a, bold line). This means that the GATA-1 sequences analyzed have been optimized by their preliminary alignment to create these traditional recognition procedures [11]. When the traditional recognition procedures were not involved (Fig. 4a, broken line), the standard deviation value is approximately K^-1/2-fold decreasing with the K value (as is stated by the Central Limit Theorem) until its alignment-dependent level is reached. Essentially, the Central Limit Theorem-established decreases are for the random DNA sequences in both variants, with and without the traditional recognition procedures (Fig. 4b). These results pinpoint that the mean recognition F_K is increasing the accuracy of a given functional site recognition through the K^-1/2-fold decrease of the standard deviation of the non-site sequences, which is responsible for the type II error a₂.

Conclusion

In this work, we introduce the idea of simultaneous involvement of as many procedures recognizing a functional site in an arbitrary DNA sequence as we can design. The simplest implementation of this idea is averaging the all partial recognizing procedures available (“mean recognition”). Unexpectedly, the analysis of the mean recognition shows that its statistical properties are described by the Central Limit Theorem. Essentially, this theorem establishes that the mean recognition F_K should became Gaussian and its standard deviation K^-1/2-decreased with the total number K of the partial recognitions averaged. We have actually observed this essential decrease (Fig. 4b). This yields that the mean recognition behavior should be predictable by the Central Limit Theorem even when each of its partial recognitions are heuristic with their unpredictable behavior. Thus, the mean recognition is the systemic approach increasing the accuracy of the functional site recognition for genomic DNA annotation.

Further development of the mean recognition approach will focus on the increase in the total number K>>100 of the averaged partial recognitions {f_k} through involvement of additional methods, such as Information Content, Perceptron, Neural Network, etc. Various weighting of the partial recognitions within the mean recognition will be also studied. Finally, it is interesting to implement the Central Limit Theorem to design the mean recognitions for increasing the accuracy of the coding potentials of exons, the non-coding potentials of introns, and the regulatory potentials of promoters [12-14].

We are grateful to Ms. Galina Chirikova for the help in translation. This work was granted by NIH 2-R01-RR04026-08A2; Russian Human Genome Project; Russian Foundation for Basic Research 97-04-49740, 96-04-50006, 97-07-90309, 98-07-90126; SB RAS IG-97N13 and the Young Scientists Awards’97/98.

References

J.W. Fickett, Trends Genet., 12, 316 (1996).
M.S. Gelfand, J. Comput. Biol., 2, 87 (1995).
P. Bucher, J. Mol. Biol., 212, 563 (1990).
S. Karlin and V. Brendel, Science, 257, 39 (1992)
K. Quandt, K. Frech, et al., Nucleic Acids Res., 23, 4878 (1995).
E.C. Uberbacher, Y. Xu, and R.J. Mural, Methods Enzymol., 266, 259 (1996).
Q.K. Chen, G.Z. Hertz, and G.D. Stormo, Comput. Appl. Biosci., 13, 29 (1997).
J.W. Fickett and A.G. Hatzigeorgiou, Genome Res., 7, 861 (1997)
M. Burset and R Guigo, Genomics, 34, 353 (1996).
Y.V. Kondrakhin, V.V. Shamin, and N.A. Kolchanov, Comput. Appl. Biosci., 10, 597 (1994)
C. Lawrence, Comput. Chem., 18, 255 (1994).
V.V. Solovyev, A.A. Salamov, and C.B. Lawrence, Nucleic Acids Res., 22, 5156 (1994).
R. Guigo and J.W. Fickett, J. Mol. Biol., 253, 51 (1995).
Y.V. Kondrakhin, et al., Comput. Appl. Biosci., 11, 477 (1995).

Figure 1. The scheme of the database SAMPLES.

Figure 2. The C-programs generated to recognize GATA-1 site using the traditional (a) consensus and (b) frequency matrix as well as (c) the novel 5 bp-consensus of the alphabet Nx₁₆ and (d) frequency matrix of the alphabet WSx₄ from Table 1. The frequency values (b) reasoning the GATA-1 consensus (d) are underlined.

Table 1. The alphabets used to construct the consensuses and frequency matrices recognizing the site

		Alphabet E_n={e₁, … . e_n} of the oligonucleotides of L length		Consensus	Freq-	Previous
Name	L	(M=A/C, K=G/T, R=A/G, Y=T/C, W=A/T, S=G/C, x=A/T/G/C)	n	threshold, f₀	uensy	usage
N₄	1	A, T, G, C	4	0.500	+	Traditional
N₁₆	2	AA, AT, AG, AC, TA, TT, …., GC, CA, CT, CG, CC	16	0.333	+	This work
N₆₄	3	AAA, AAT, AAG, …., CGC, CCA, CCT, CCG, CCC	64	0.125	–	[10]
Nx₁₆	3	AxA, AxT, AxG, AxC, …., GxC, CxA, CxT, CxG, CxC	16	0.333	+	This work
Nx₆₄	5	AxAxA, AxAxT, AxAxG, …., CxCxT, CxCxG, CxCxC	64	0.125	–	This work
MK₄	2	MM, MK, KM, KK	4	0.500	+	This work
MK₈	3	MMM, MMK, MKM, MKK, KMM, KMK, KKM, KKK	8	0.250	+	This work
KM₁₆	4	MMMM, MMMK, MMKM, MMKK, …, KKKM, KKKK	16	0.333	+	This work
MKx₄	3	MxM, MxK, KxM, KxK	4	0.500	+	This work
MKx₈	5	MxMxM, MxMxK, MxKxM, MxKxK, …, KxKxM, KxKxK	8	0.250	+	This work
RY₄	2	RR, RY, YR, YY	4	0.500	+	This work
RY₈	3	RRR, RRY, RYR, RYY, YRR, YRY, YYR, YYY	8	0.250	+	This work
RY₁₆	4	RRRR, RRRY, RRYR, …, YYRR, YYRY, YYYR, YYYY	16	0.333	+	This work
RYx₄	3	RxR, RxY, YxR, YxY	4	0.500	+	This work
RYx₈	5	RxRxR, RxRxY, RxYxR, RxYxY, …, YxYxR, YxYxY	8	0.250	+	This work
WS₄	2	WW, WS, SW, SS	4	0.500	+	This work
WS₈	3	WWW, WWS, WSW, WSS, SWW, SWS, SSW, SSS	8	0.250	+	This work
WS₁₆	4	WWWW, WWWS, WWSW, …, SSSW, SSSS	16	0.333	+	This work
WSx₄	3	WxW, WxS, WxS, SxS	4	0.500	+	This work
WSx₈	5	WxWxW, WxWxS, WxSxW, …, SxSxW, SxSxS	8	0.250	+	This work

Table 2. The partial and mean recognizing procedures generated for GATA-1 and C/EBP sites

Recognition procedure			GATA-1 (51 sequences, control)				C/EBP (99 sequences, control)
	Name	Type	site, mБ d	a ₁	rand, mБ d	a ₂	site, mБ d	a ₁	rand, mБ d	a ₂
Traditional	N₄	Freq	0.80Б 0.48	0.04	-1.02Б 0.52	0.04	0.93Б 0.47	0.05	-0.99Б 0.56	0.05
Traditional	N₄	Cons	0.80Б 0.63	0.02	-1.09Б 0.63	0.07	1.05Б 0.46	0.02	-0.83Б 0.62	0.11
Best for C/EBP	N₁₆	Freq	0.74Б 0.48	0.08	-1.05Б 0.30	0.01	0.90Б 0.55	0.06	-1.12Б 0.43	0.02
Best for GATA-1	N₁₆	Cons	0.87Б 0.67	0.04	-1.04Б 0.35	0.02	1.12Б 0.75	0.10	-0.94Б 0.49	0.03
Introduced in [10]	N₆₄	Cons	0.89Б 0.84	0.08	-0.96Б 0.20	0.02	1.16Б 1.15	0.13	-0.96Б 0.42	0.07
Examples of novel	WS₄	Freq	0.86Б 0.48	0.06	-0.92Б 0.66	0.09	0.79Б 0.73	0.13	-0.82Б 0.81	0.16
alphabets usage	WSx₄	Freq	0.87Б 0.55	0.08	-0.92Б 0.70	0.09	0.84Б 0.80	0.13	-0.97Б 0.87	0.14
Only novel averaged			0.78Б 0.64	0.08	-1.00Б 0.33	0.02	1.01Б 0.53	0.03	-0.98Б 0.41	0.03
Mean Recognition			0.78Б 0.63	0.08	-1.00Б 0.34	0.02	1.01Б 0.52	0.03	-0.98Б 0.42	0.03


Figure 3. The “mean recognition” of (a) GATA-1 and (b) C/EBP sites (“Mean”) decreases both type I and II errors, a₁ and a₂, compared to traditionally used method of frequency matrix (“Traditional”)


Fig. 4. The standard deviation of the mean recognition score is decreasing with the total number of the partial recognitions averaged over (a) the site analyzed and (b) the random DNA, as predicted by the Central Limit Theorem.