The Institute of Medical Science, The University of Tokyo, 4-6-1 Shirokane-dai, Minatoku, Tokyo 108, Japan; e-mail:tatsu@ims.u-tokyo.ac.jp; e-mail:takagi@ims.u-tokyo.ac.jp
+Corresponding author
Keywords: transcription factor, genetic networks, gene function, transcription regulation, database
Precise analysis of genetic network, gene function, and transcription regulation requires accurate prediction of transcription factor (TF) bindability on DNA. We generalize the concept of local over-representation with statistical measure, and propose a new algorithm for deciding cut-off for matching score of TF weight matrix on DNA using background rate estimated on non-promoters. The method is finally applicable to 96.5% vertebrate TFs in the database TRANSFAC. The result suggests that TFs, GC box for example, have multiple binding sites spreading over promoter area wider than generally considered; the set of local over-representative promoters for each TF varies with window position. This suggests a new view that promoters must be locally classified depending on each local preferential site.
1. Introduction
How precise we can predict TF-DNA interaction largely affects followings: (i) There are so many kinds of TFs that it is hard to examine experimentally which TFs interact with each TF. However, if we can accurately examine TF binding sites on DNA, and if combinations of the binding sites are conserved on many promoters, we can identify the interaction between these TFs ([1]). From such TF binding patterns on promoters, we can see how TFs regulate transcription. (ii) TF binding sites on the DNA are effective clue for predicting promoter regions on DNA, because we can compare the patterns and density of TF binding sites on them with those on non-promoters ([2]). (iii) Gene function can be identified by factor response and organization specificity of its upstream promoter. Thus, we must examine which TFs control the transcription by binding with the promoter region, enhancer, silencer, and so on ([2][3]). (iv) Analyzing intra-cell and inter-cell pathway, protein-protein interaction, ligand/domain interaction, and TF (protein) -DNA interaction can predict how genetic networks regulate the expression of RNA and protein.
To identify TF binding sites on DNA, we have to specify each DNA-binding-motif (e.g., in weight matrix form), calculate matching score between the motif and input sequences, and separate them from non-binding sites with cut-off for the score. For getting each TF motif, we use data from TF database such as TRANSFAC. For calculating the score, we use the standard method ([4]). While, cut-off for the matching score of each TF is unknown yet. Therefore, it is necessary to fix each cut-off; this research aims to propose a new algorithm for fixing them. For this, we can use position specificity of TF binding sites. Transcription starts when RNA Pol II binds with the transcription start site (TSS) on DNA. The Pol II is aligned by result of various kind of interaction between TFs such as complex-formation, activation, inactivation, and so on. That is, gene expression is regulated by the activation of TFs and interaction between them. Because the group of interacting partners of each TF is limited, and because the 3D spatial condition for TF-TF interaction is restricted, TF binding patterns are supposed to be conserved on many promoters evolutionary if it has functional meaning, so that they can satisfy their mutual restriction.
We can find a research that aims to get DNA binding motif of each TF (T), cut-off value of its binding score, and its preferred binding region on DNA ([4]) using such position specificity of TF binding sites. The method takes the following procedures: First, it aligns many promoters with the TSS. Assume it can temporarily fix the motif to some pattern and the cut-off to some value. Consequently, it can find the region of preferential occurrence (P) of T’s binding sites on promoters, and background region (B) complementary to P. T’s binding probability (normalized by the length of P) on P is defined as signal. T’s binding probability (normalized by the length of B) on B is defined as background. And the difference between signal from background is defined as local over-representation. The motif and the cut-off are adjusted so that they maximize the local over-representation. That method assumes that the promoter area can be clearly separated into two areas (the signal area and the background area) according to the motif and cut-off. However, this assumption is sometimes wrong. One critical case is that there is no background area because the whole promoter region is signal area in fact. In this case, the separating procedure itself is wrong. Another case is that only one preference region is considered as signal area, although, besides it, there are several signal areas on promoters, which are mistaken as background areas. Consequently, that method sometimes falls into local minimum. To avoid it, parameters must be carefully tuned. But it requires much labor. Moreover, the result is sometimes wrong.
Therefore, we modified some concepts: First of all, instead of using background rate estimated on promoter region, we estimated background on non-promoter sequences. Next, to estimate local over-representation on all of multiple preferred regions on promoter, we introduce a local window at every position. In the window, the number of promoters with TF binding sites is counted. Thereafter, statistical significance of the occurrence compared to background fluctuation is calculated. We call this amount generalized local over-representation. Based on this, we introduce the fixing algorithm for cut-off: If some value is set for the cut-off, set of given promoters can be separated into two sets: promoters with TF binding sites in the window, and promoters without TF binding site in the window. The optimum cut-off is the maximum value that satisfies the condition that the latter set does not have local over-representation for any hypothetical cut-off potentially. Our algorithm is applied to 202 vertebrate TFs in TRANSFAC and the cut-off of 195 TFs can be decided. The threshold can be fixed without any initial-parameter-tuning by hand.
2. Method
2.1 New concepts
(1) We introduce a local window of width w that centers on position x bp upstream of the TSS. The number of promoters with TF binding sites within the window is counted as coincidence.
(2) We define generalized local over-representation as following statistical amount:
Og =(the number of coincident cases – background) /(standard deviation of background).
Here, the number of coincident cases is the number of coincident occurrences within the window, and the background is estimated value according to the number of initially given samples. When Og > Oc (e.g. 2.0) is satisfied, we consider there is significant local over-representation.
(3) By aligning the set of all given promoters with TSS, we assume they can be locally (within each window) separated into the following two sets: (a) promoters that have TF binding-sites within the window and (b) other promoters. Our final goal is to get the maximum cut-off with which (a) and (b) satisfy the following condition: Set (b), which is exclusive set of (a) and once fixed for the cut-off value, keeps the number of TF binding promoters less than background fluctuation at any hypothetical threshold. —(*)
2.2 Background estimation by Poisson distribution
(1) The TF’s binding probability p/1bp1sequence is estimated on non-promoter sequences. (2) The binding probability of the TF within w bp (on one sequence) = 1 – p(0|wp) = 1- e-wp (Poisson distribution is assumed: ![]() . (3) Thus, if k sequences are given, the number of sequences on which TFs bind (background rate) is estimated to be k (1-e-wp). (4) By Poisson distribution, standard deviation of the background rate is
. (3) Thus, if k sequences are given, the number of sequences on which TFs bind (background rate) is estimated to be k (1-e-wp). (4) By Poisson distribution, standard deviation of the background rate is ![]()
2.3 Algorithm
Align all sets of promoters with the TSS. Suppose Oc = 2.0(fixed for any condition). Following procedures are applied to every factor respectively.
Initially, set the cut-off th to 1.0.
List up all candidates of TF binding sites on all promoters for the cut-off value.
Consider window W of width w at position x upstream of TSS.
Examine the TF bindability on each promoter. Assume promoters TF bindable within the window = {P1, P2, P4} (set (a)), and promoters not TF bindable within the window = {P3, P5} (set (b)).
Assume background rate for 5 promoters 0.8, and its standard deviation 0.9. Since the set (a) satisfies the condition Og = (3-0.8)/0.9 > Oc, this set has local over-representation within this window at this cut-off value.
Next, we check whether the set (b) has local over-representation potentially by following steps:
a. On the two promoters in the set (b), TF binding sites estimated with a certain cut-off th’ (e.g. 0.8) lower than th are listed up. Assume background rate 0.2 for 2 promoters (set (b)), and the standard deviation 0.45.
b. Within the same window, the number of promoters (in the set (b)) TF bindable is counted.
c. Assume the number is 2 for example. Because the number satisfies the condition Og= (2-0.2) / 0.45> Oc, the set (b) has local over-representation potentially. Thus this set does not satisfy the criteria (*). Reduce the cut-off value th with some step size, e.g. 0.01, and go to 3.
d. If the result of 7b is 1, Og=(1-0.2)/0.45< Oc (as the background rate is the same of 7c). Thus we can see no local over-representation potentially with this cut-off th’ within this window. If the above criteria is satisfied for every situation (0<=th'<=th, wmin<=w<=wmax), go to next step.
The final cut-off value is the minimum one calculated by the procedure above at all positions.
3. Experimental Results
We used databases and parameters as follows: (a) we used 202 vertebrate TFs from database TRANSFAC Ver.3.3 [5]. With the weight matrix data in it, each TF matching score (binding score) in each position is calculated according to Bucher’s method ([4]). (b) We used EPD R.50 [6] for promoter sequence investigation. Non-redundant sequences were taken out from the mammalian promoters. Among them, we finally used 266 promoters in which region of -349-+100bp to TSS is determined. (c) From genbank, we extracted sequences of total 664,505 bp (1,329,010 bases) according to the list of non-promoter that Dr.Prestridge of the Minnesota University [7]. (d) wmin = 1, wmax = 9. (e) Oc = 2.0. (f) Minimum number of coincident cases (TF bindable promoters) when local over-representation is calculated = 4. (f) Step size for reducing cut-off = 0.01.
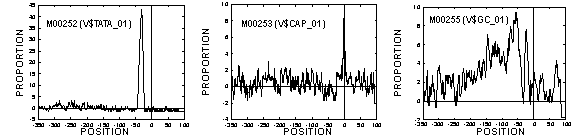
Applying our method to TRANSFAC data, we could fix 195 of 202 vertebrate TFs including typical TFs listed in Table 1. Example spectra of TATA box, cap site, and GC box are shown in Fig. 1. The program is written in C++ and is executable on a supercomputer (Sun Enterprise 10000, 64 CPU parallel) at the Human Genome Center.
Table 1. Fixed cut-off for %matching score of each TF weight matrix (typical examples). It also shows #accession and id in TRANSFAC, cut-off, preferential area (only top) to TSS, and #promoters in the area.
|
#ACCESS |
FACTOR ID |
CUT-OFF |
P.area (top) |
#pro |
|
M00008 |
V$SP1_01 |
79 % |
-115 : -33 |
235 |
|
M00255 |
V$GC_01 |
79 % |
-107 : -31 |
197 |
|
M00252 |
V$TATA_01 |
78 % |
-46 : -23 |
179 |
|
M00189 |
V$AP2_Q6 |
79 % |
-29 : -2 |
140 |
|
M00176 |
V$AP4_Q6 |
76 % |
-33 : -4 |
128 |
|
M00253 |
V$CAP_01 |
84 % |
-3 : 1 |
116 |
|
M00254 |
V$CAAT_01 |
80 % |
-107 : -66 |
111 |
|
M00083 |
V$MZF1_01 |
83 % |
-66 : -30 |
99 |
|
M00232 |
V$MEF2_03 |
72 % |
-45 : -31 |
71 |
|
… |
… |
… |
… |
… |
Figure 1 Spectra of TATA box (TBP binds)(left), cap site (TSS)(middle), and GC box (Sp1 binds)(right). Both are taken using the fixed cut-offs. Y-axis shows Og (ratio of signal to background-fluctuation within local window at each position).
4 Discussion
It is GC box (Sp1 binding site) that the difference between our method and the past research ([4]) is remarkable. The cut-off adjusted by that method is higher than our result. The reason is that there are multiple preferred areas of GC box over the entire promoter area. In his method, the region considered to be signal area (other areas are thus considered to be background area) largely depends on initial values of parameters. Using initial setting in that literature, it could catch only area that the occurrence is the highest. Therefore, it estimated background and thus cut-off too high, and preference region too narrow.
While, in our method, because background rate is estimated on non-promoters, and because the criteria of local over-representation had been set at each position over the full area, it avoided above mistake. In fact, preference site is not clear, and not specified as one; therefore, we took an approach that local over-representative promoters are decided locally. Because we separated a whole set of promoters into local over-representative promoters in a local window and non-local-over-representative promoters in the window, the definition of signal and background becomes clear and produced merit that the discrimination can be used to classify promoters locally. In the procedure, our system checked local windows with every width at each position, because it can vary according to the binding density fluctuated by width and position of the window. Also, because the background rate is decided from non-promoter sequences, the algorithm does not have to discriminate signal area from background area on promoter sequences. As a result, the thresholds of almost most factors (195/202) could be specified without any hand-tuned initial value.
Next, we discuss limitation of our work: Firstly, there may be cases that the algorithm can not deal with factors whose binding sites are sparsely spreading over promoters. For example, although the coincidence rate is within a range of random coincidence level locally, it might exceed the random level globally. Such positional shift of binding sites may arise from gap propagation between TFs and more complex mechanism such as dynamic structural changes, e.g., DNA bending. Since we set the maximum limit of the window width as 9bp, such global over-representation cannot be caught. Although it is possible to deal with wider local over-representation by setting the limit larger, we still have the problem that it requires much time for the trial and for estimating background rate. Secondly, there are TFs that bind on DNA too rarely to catch the local over-representation, or TFs that do not have such coincidence on promoters at all. These are causes that the thresholds of seven TFs were not decided. Finally, there are some TFs that miss-recognized TATA box because the consensus sequences are very similar to TATA box. If they have other preference regions, their cut-off can be tuned on them. However, the cut-offs might be estimated rather low because they must satisfy the criteria also on the miss-recognized TATA box.
5 Conclusion
Statistical data mining from large database contributes much to phenomena where experimental knowledge is still poor. Bucher’s method showed its power. We improved and generalized the idea of local over-representation and proposed the instance discriminating algorithm: Set of all instances can be separated into two following sets in the window (local region in phase space) at each position. (a) Set of instances with local over-representation, and (b) set of instances without local over-representation. No matter how the parameter (e.g. cut-off) values are changed, the set (b) does not have local over-representation in the window. This concept can be generally applied to events counted as frequency in a window of phase-space (spatial and temporal) such as protein-DNA interaction, protein-protein interaction, ligand/domain docking, network causality, and sequences which are conserved in the evolution to use their interaction. This paper proposed how to apply the method for fixing cut-off for matching score of each TF weight matrix in TRANSFAC; cut-offs of 195 vertebrate TFs were determined. With this result, we can classify promoters according to various kind of gene expression and gene function, predict their region on DNA and their regulating function, and clarify TF-DNA interaction in genetic networks.
References
- T. Tsunoda and T. Takagi, “Automatic Extraction of Position Specific Cooccurrence of Transcription Factor Bindings on Promoters” PSB-98, 252-263 (1998)
- J. W. Fickett and A. G. Hatzigeorgiou, “Eukaryotic Promoter Recognition” GENOME RESEARCH 7, 861-878 (1997)
- W. Fujibuchi and M. Kanehisa, “Prediction of Gene Expression Specificity by Promoter Sequence Patterns” DNA RESEARCH, 4, 81-90 (1997)
- P. Bucher, “Weight Matrix Descriptions of Four Eukaryotic RNA Polymerase II Promoter Elements Derived from 502 Unrelated Promoter Sequences” J. Mol. Biol. 212, 563-578 (1990)
- T. Heinemeyer et al. “Databases on Transcriptional Regulation: TRANSFAC, TRRD, and COMPEL” Nucl. Acids Res. 26, 364-370 (1998)
- R. Cavin, T. Junier, and P. Bucher (1997). The Eukaryotic Promoter Database EPD, Release 50. Swiss Institute for Experimental Cancer Research, 1066 Epalinges s/Lausanne, Switzerland.
- D. S. Prestridge, “Predicting Pol II promoter sequences using transcription factor binding sites” J. Mol. Biol. 249, 923-932 (1995)