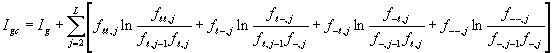HERTZ GERALD Z.+, STORMO GARY D.
Department of Molecular, Cellular, and Developmental Biology; University of Colorado; Campus Box 347; Boulder, CO 80309; USA; hertz or e-mail: stormo@colorado.edu
+Corresponding author
Keywords: patterns, statistically significant alignment matrix, information context
We have been developing computational methods for identifying consensus patterns in sets of DNA or protein sequences that are functionally related according to previous experiments. For example, functionally related DNA sequences can be coordinately regulated promoters, or DNA sequences that are bound by a common protein. Our methods align the functionally related sequences to identify the consensus pattern. Once a pattern is identified, it can be used to predict related domains in other sequences.
We describe consensus patterns with alignment matrices that summarize a sequence alignment. We use various matrix models that range from simple ungapped patterns to complex patterns containing gaps (i.e. insertions and deletions) and adjacent correlations. Alignment matrices are initially compared using a log-likelihood score we call information content. However, the ultimate statistical significance of an alignment is the product of the p-value of its information content and the number of alignments that can be created from the data. Previously, we have been able to determine good estimates of the number of possible alignments due to the data. Here, we introduce a method for accurately estimating the p-value of the information content of an alignment matrix.
1. Describing sequence alignments with matrices
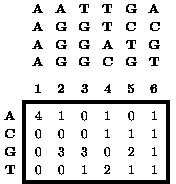
Figure 1 An example of a matrix summarizing a DNA sequence alignment not containing gaps. On the top is an alignment of four 6-mers. Below is a matrix containing the number of times that the indicated letter is observed at the indicated position of this alignment.
Functionally related DNA and protein sequences are generally expected to share some common sequence elements. For example, a DNA-binding protein is expected to bind related DNA sequences. The pattern shared by a set of functionally related sequences is commonly identified during the process of aligning the sequences to maximize sequence conservation. The oldest method for describing a sequence alignment is the consensus sequence, which contains the most highly conserved letter (i.e. base for DNA or amino acid for protein) at each position of the alignment. However, most alignments are not limited to just a single letter at each position. At some positions of an alignment any letter may be permissible, although some letters may be much more frequent than others. A more complete description of an alignment is the alignment matrix, which, in its simplest form, lists the occurrence of each letter at each position of the alignment (Figure 1).1 However, alignment matrices can also describe more complex patterns that contain gaps (i.e. sequences contain insertions and deletions relative to each other) or in which different positions are correlated with each other (Figure 2).2
Figure 2. An example of a matrix summarizing a DNA sequence alignment that contains gaps. On the top is an alignment of four sequences: the first and last are 6-mers, and the middle two are 4-mers. Below is a matrix whose first five rows represent our simplest matrix for alignments containing gaps. The first four rows contain the number of times that the indicated letter is observed at the indicated position of this alignment, and the fifth row contains the number of times that a gap is observed at the indicated position. A more complex matrix representation includes gap-letter correlations and contains the four lower rows showing the number of times that a letter (
) or a gap (- ) is preceded by a letter or a gap.
2. Measuring sequence conservation with information content.
2.1 Information content of a simple alignment
We score the significance of a sequence alignment by what we call the information content of the alignment matrix.1,2 The higher the information content, the rarer the pattern described by the alignment. The following is the formula for determining the information content 
of a simple alignment matrix (Figure 1):
|
|
(1) |
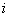refers to the rows of the matrix (e.g., the bases A,C,G,T for a DNA alignment),
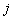refers to the columns of the matrix (i.e., the position within the pattern),
is the total number of letters in the sequence alphabet (4 for DNA and 20 for protein),
is the total number of columns in the matrix,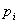
is the a priori probability of letter 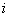– this might be the genomic frequency in the particular organism or the observed frequency in the particular data set and
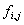is the frequency that letter 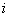occurs at position 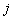so that 
.
The minimum value of is 0. An alignment having this minimum value is consistent with a pattern that any sequence might match. When is at its maximum value, only a single sequence will be consistent with the pattern.
This formula for information content assumes that each position of the alignment is independent and that each column of an arbitrary alignment of random sequences follows a multinomial distribution. The most conventional derivation of formula 1 is to simply normalize the negative of the common log-likelihood statistic (described in introductory statistics books) by the number of sequences in the alignment. Alternatively, the formula can be shown to be a large-deviation rate constant.3
2.2 Information content of alignments containing gaps
The information content 
of an alignment containing gaps but no correlations (first 5 rows of the matrix in Figure 2) includes an additional term 
, which is the frequency of a gap occurring at position of the alignment, so that 
. The formula for is:
 |
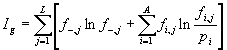(2) |
Notice that the formula 1 can be derived from formula 2 by setting 
because 
. Also notice that any column in which 
(i.e., the corresponding position never contains any letters) contributes nothing to the overall value of . Thus, an infinite number of meaningless positions containing only gaps can be added to any alignment without altering its information content.
There is no a priori probability for gaps since they can be freely introduced. For example, the a priori probability of a sequence is not altered by inserting gaps into its alignment. However, because gaps can be freely inserted into the alignment, the number of permissible alignments is greatly increased. The derivations, mentioned for the information content of alignments not containing gaps, can be generalized to alignments containing gaps.
2.3 Information content of alignments containing adjacent correlations
Gaps are frequently clustered in adjacent positions of an alignment. In extreme cases of clustering, a pattern containing gaps can be described as multiple ungapped conserved domains separated by variable length unconserved spacer sequences. Information for clustering gaps is contained in the correlations between adjacent letters and gaps (the last 4 rows of the matrix in Figure 2). The information content 
for such an alignment is
,
in which 
is the frequency of a letter instead of a gap occurring at position ; and 
, 
, 
, 
are the frequencies of adjacent gaps and letters. For example, is the frequency of a gap at position following a letter at position 
.
The bracketed term in the summation is commonly called mutual information and represents the information content due to the adjacent correlations between the occurrences of gaps and letters. The mutual information is at its minimum value of zero when the frequencies of adjacent letters and gaps are independent – i.e., the four fractions are each equal to one. This last alignment model is very similar to the most common hidden Markov models used for determining and describing protein sequence alignments.
3. Determining the p-value of the information content
Information content is a good measure for comparing alignments having the same width and the same number of sequences. However, a more meaningful measure is the p-value of the information contentói.e., the probability of observing an information content greater than or equal to a specified value, given the width of the alignment and the number of sequences in the alignment. The p-value also allows the comparison of alignments having different widths and containing different numbers of sequences. When calculating p-value, our null model is that the distribution of letters in each alignment column is an independent multinomial distribution in which the probability of observing each letter is the a priori probability of that letter. We calculate the p-value of an information content 
using a technique from large-deviation statistics.3 Let 
be the probability of observing an information content . Define a new probability 
as
 , where |
(4) |
is the moment generating function for and ensures that 
; 
is chosen such that the average of for 
is : 
; and the variance of for 
is 
. Formula 4 can be rearranged so that
, and
 |
(5) |
Formula 5 became useful for estimating p-value once we realized that 
, 
, and 
can be determined in time 
for the alignment models described in sections 2.1 and 2.2. Thus, can be determined numerically, the bracketed portion of equation 5 can be determined exactly, and the summation can be approximated by a normal distribution.
An accurate estimation of p-value is necessary since the ultimate statistical significance of an alignment is the product of the p-value and the typically huge number of alignments that can be generated with any set of data. For example, given 
sequences of length 
, the number of alignments of width and having a single contribution from 
of the sequences is 
. Alternative formulas for counting alignments also exist for when each sequence is not limited to contributing at most once to any single alignment.
5. Conclusion
We have described how alignment matrices and information content can describe and score simple ungapped alignments and complex alignments having gaps and adjacent correlations. We also described how to determine the statistical significance of an alignment and introduced a new method for determining the p-value of alignments in which each column is considered independent. Extending this method for estimating p-value to our more complex alignment models that incorporate adjacent correlations is in progress.
Acknowledgments
This work was supported by Public Health Service grant HG-00249 from the National Institutes of Health.
References
- G. Z. Hertz, G. W. Hartzell III, and G. D. Stormo, “Identification of Consensus Patterns in Unaligned DNA Sequences Known to be Functionally Related” Comput. Appl. Biosci. 6, 81ñ92 (1990)
- G. Z. Hertz and G. D. Stormo, “Identification of Consensus Patterns in Unaligned DNA and Protein Sequences: A Large-Deviation Statistical Basis for Penalizing Gaps” In Proceedings of the Third International Conference on Bioinformatics and Genome Research, H. A. Lim and C. R. Cantor, editors, pages 201ñ216 (World Scientific Publishing Co., Ltd., Singapore, 1995)
- J. A. Bucklew, “Large Deviation Techniques in Decision, Simulation, and Estimation” (John Wiley and Sons, Inc., New York, 1990)