TRIPLET PERIODICITY OF THE DNA CODING AND NONCODING REGIONS

RUDENKO V.M.+, KOROTKOV E.V.

Centre “Bioengineering”, Russian Academy of Sciences, Prospect 60-tya Oktyabrya, 7/1, 117322, Moscow, Russia;
e-mail: korotkov@biengi.msk.su, Fax:7-095-135-05-71;

+Corresponding author

Keywords: nucleotide sequences, triplet periodicity, strong base correlations, mutual information

Introduction

The study of a periodicity of DNA sequences is very important for understanding of a DNA sequence structure and for developing of methods for identification coding regions. Now a search of a DNA periodicity is mainly based on the analysis of homological periodicity including imperfect repeats (1,2,3,4,5,6). However, a latent periodicity of DNA sequence may exist and it is hard or impossible to find a latent periodicity by the algorithms developed. For example, in DNA sequence may be observed the triplet period (A/C/T)(T/G)(G/A), where the first position of a period contains A, C or T, the second position contains T or G and so on. The lot of DNA sequences can contain the one type of the latent periodicity. The example of the sequences with this type of the latent periodicity is: [ATG][CGA][TTA][CGA][ATA]…There are many types period of a latent triplet periodicity and the gomology between the DNA sequences with same type of latent periodicity may be low or absent. Early we have developed a mathematical method for search of a latent periodicity in DNA sequences (7, 8, 9). The application of this method for analysis DNA sequences permits to find long latent periodicity of about 20% of known genes. The purpose of this report is to find all regions from human coding and noncoding regions with triplet periodicity and attempt to find correlation between presence a coding region and a latent triplet periodicity in DNA sequence. Early in many publications (see for review 10,11,12) it was found a strong base correlations in DNA coding regions and it is a base for introduction of many coding potentials. The another task of this work is classifications of triplet periodicity that occurs in DNA coding regions and determination main triplet periodicity types that can be found in coding regions. Using the results of this work we can find more 50% of the coding regions with the probability of a mistake less than 0.6%. The search time of the triplet latent periodicity in 105 b.p. is less than 2 minutes.

Methods and Algorithms

We selected all coding and noncoding regions from last version of EMBL data bank. There are 17167 coding and 22282 noncoding regions with the length more than 200 b.p. For search of the triplet latent periodicity we used the window equal to 200 base pairs and this window was scanned across the coding and noncoding regions. We compared the artificial periodic sequences with the DNA sequence for search latent periodicity (7, 8, 9). Alphabet of artificial sequences contains 3 letters (S1, S2, S3) and the sequence S1S2S3S1S2S3S1S2S3… is generated. The length of the artificial sequence is equal to the length of the analysed sequence. Mutual information is chosen as measure of similarity of artificial and DNA sequences. A matrix M(3,4) is filled in for calculation of the mutual information. Elements of the matrix M are the numbers of coincidences of each type between the artificial sequence and the DNA sequence compared. The dimension of matrix M is 3×4. The labels of the rows of the matrix M are the bases A, U, C and G. Labels of the columns of the matrix M are the letters Si (i=1,2,3) of the artificial sequence. Sums of elements in the rows are equal to the quantity of A, U, C and G bases in the DNA sequence. The sums of elements in each column are equal to the quantity of Si letters in the artificial sequence. The mutual information is calculated using the formula (13):

(1)

Here i is changes from 1 to 3 and j is changes from 1 to 4; mij is the element of a matrix M; xi is the quantity of each A, U, C and G symbol in the mRNA sequence; yj is the quantity of the Sj symbol in the artificial sequence; L is the length of compared sequences. The 2I value is distributed as c 2 with 6 degrees of freedom. It permits us to evaluate the probability of accidental formation of triplet periodicity.

We tested the conformity of the 2I distribution to the c 2 distribution with 6 degrees of freedom. We compared artificial sequences of different lengths with 5×106 base pairs of random sequence. If the length of the artificial sequence was more than 30 b.p. then the 2I distribution corresponds to the c 2 distribution with 6 degrees of freedom with probability no less than 99%. Using formula (2) we transformed the mutual information to argument of normal distribution.

(2)

We selected the sequences in each coding or noncoding DNA region with the maximum of X. If X was more than 5.0 than we chosen this sequence as sequence with latent periodicity. It gives the probability to find “random” triplet periodicity less than 10-6. Corresponding M(3,4) matrix was considered as type of the found latent triplet periodicity. We used the c 2 as the measure of similarity between different M(3,4) matrixes and executed the comparison between any two matrixes for all found sequences.

(3)

here – mkij – (i,j) element of Mk(i,j) matrix; nk – sum of elements of two compared matrixes, k is 1 or 2. X2 is distributed as  2(11). For the classification of M(3,4) matrixes we executed the next procedure.

We considered each matrix as the centre of class and compared it with all matrixes. If obtained value X2 was less than the chosen level we assume that these two matrixes belong to the same class.

  1. From obtained classes we found that one, that had most elements of all. Than we continued the classification for all matrixes that did not enter in this class.

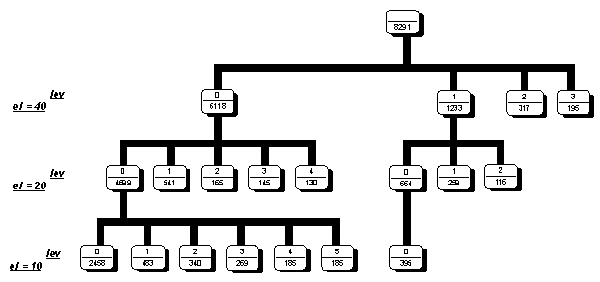
We used this method for classification M(3,4) matrixes form coding regions. The first level of X2 was taken as 40.Than obtained on this step classes were divided on level 20 and 10. Results of classification is shown on Fig.1. Each node of the classification tree is a class. Number in the upper part of the node is a class number, second number is the volume of the class. In figure we show those classes which contain no less than 5% of all classified matrixes.

Figure 1. Classification scheme of M(3,4) matrixes for coding regions.

Results and Discussion

This analysis revealed 8921 regions with triplet periodicity from coding regions and 386 regions with triplet periodicity from noncoding regions. The X value was varied from 5.0 to 15.0. The noncoding regions from EMBL data bank can contain the unknown coding regions and pseudogenes. To select true noncoding regions with triplet periodicity we compared all found sequences with triplet periodicity from the noncoding regions of EMBL data bank (386 sequences) with the all coding sequences. We used the FASTA algorithm for this purpose. The weight of AA, TT, CC and GG coincidences was equal 4 and weight of other coincidences was equal to -1. We scanned all coding regions from human clones and searched the gomology with the weights more 210. It gives the probability of random coincidence between DNA sequences less than 10-8. The 321 regions with triplet periodicity have the gomology with coding regions. It shows that the most part of the found triplet periodicity regions from noncoding sequences is the unknown genes or pseudogenes and the probability of wrong prediction of a coding regions or pseudogenes on the base of the triplet periodicity is low that 0.6%. We show as example the gomology between noncoding sequence with triplet periodicity from intron C of the HSTPO04 clone of EMBL data bank and the coding sequences of the trichohyalin gene of HSTRHYAL clone (Fig.2). HSTPO04 clone contains the human thyroid peroxidase gene. X is equal to 8.7 for the sequence with latent triplet periodicity. These sequences have 64% gomology. It shows that the part of sequence of the intron C can execute a coding function and intron C can contain the insertion of a pseudogene.

1951-tGCAGgTGAGGaGaGgcCtGCAGgTGgGGtGaGgcCtGCAGgTGAGGgGaGgcCtGCAGgTGAG
3536-aGCAGcTGAGGcGcGagCaGCAGcTGaGGcGcGagCaGCAGcTGAGGcGcGagCaGCAGcTGAG

GgGaGgcCtGCAGgTGAGGaGaGgcCtGCAGgTGgGGtGaGgcCtGCAGgTGgGGtGaGgcCtGCAGgT
GcGcGagCaGCAGcTGAGGcGcGagCaGCAGcTGaGGcGcGagCaGCAGcTGaGGcGcGagCaGCAGcT

GAGGgGaGgcCtGCAGgTGAGGaGaGgcCtGCAGgTGAGGaGaGgcCtGcAGGtGGgGtGaggCctGC-2151
GAGGcGcGagCaGCAGcTGAGGcGcGagCaGCAGcTGAGGcGcGagCaGgAGGaGGaGaGgcaCgaGC-3736

Figure 2 Homology between noncoding sequence with triplet periodicity from HSTPO04 clone and coding sequence of the trichohyalin gene of HSTRHYAL clone. Coordinates sequences in clones are shown at the left and right boards of the sequences.

There is the probability that remainder (65 regions) belong to coding regions also but the gomology sequences are absent in human coding regions from EMBL data bank of last version. The part from 65 sequences may be ancient microsatellite with big number of mutations and a perfect periodicity between periods in this part of the 65 sequences is lost.

Results of classification shows the presence of the main type triplet latent periodicity (Fig.1). In the level of  2 equals to 40 we have the 4 main latent triplet periodicity classes and minor classes with the number sequences less than 5% of total volume of triplet periodicity regions. The biggest class contains 6118 case. In the level 20 the biggest class is divided into 5 main subclasses and biggest subclass of this level contains 4699 cases. In the level 10 subclasses is divided of additional 5 main subclasses with relatively same number of cases and big number of additional minor subclasses. The results of classification show the presence of main types of the triplet periodicity in the human coding regions.

We investigated the coding regions where we did not found triplet periodicity with X>5.0 in window that is equal to 200b.p. For these coding regions we selected the length of window equals to the length of coding region and found the left and right border positions in the window that gave X>5.0. We found the additional number of coding regions (X>5.0) with triplet periodicity equals to 2872. Than the total number of the coding regions with triplet periodicity is equal to 11793 that corresponds to 69% of the all tested coding regions from human clones. We found also that about 15% of the remaining coding regions have the triplet periodicity with 4.0<X<5.0. So, we can determine about 84% of all coding regions with different degree of the authentic.

According to obtained results the latent triplet periodicity can be considered as suitable coding potentials for very fast computer search of the unknown coding regions and pseudogenes and for the prediction of a gene function. The additional selection between genes and pseudogenes can be provided on the base of search of a promoter sequence and exon-intron sites.

References

  1. E.A.Cheever, G.C.Overton, D.B.Searls “Fast Fourier transfor-based correlation of DNA sequences using complex palne encoding”, Cabios, 7, 143, (1991)
  2. V.Ju.Makeev, V.G.Tumanyan “Search of periodicities in primary structure of biopolymers: a general Fourier approach”. Comput. Appl. Biosci. 12,49 (1995).
  3. G.Benson “Sequence alignment with tandem duplications” J.Comput. Biol. 4,351 (1997)
  4. H.Hersel, I.Grobe “Measuring correlations in symbol sequences” Physica A 216, 518 (1995)
  5. H.Hersel, W. Ebeling, A.O.Schmitt “Entropies of biosequences: the role of repeats”, Physical review E, 50, 5061 (1997)
  6. D.Arquest, C.J.Michel “Periodicities in coding and noncoding regions of the genes” J. Theor. Biol., 143, 307, (1990)
  7. E.V.Korotkov, M.A.Korotkova “DNA regions with latent periodicity in some human clones” DNA Sequence. 5, 353 (1995)
  8. E.V.Korotkov, D.A.Phoenix “Latent periodicity of DNA sequences of many genes” In: Proceedings of Pacific Symposium on Biocomputing 97. Maui, Hawaii, USA: Word Scientific Press. p.222 (1997)
  9. E.V.Korotkov, M.A.Korotkova, J.S.Tulko “Latent sequence periodicity of some oncogenes and DNA-binding protein genes” Comput. Appl. Biosci. 13, 37 (1997)
  10. J.W.Fickett “Finding genes by computer: the state of the art”. TIG, 12, 316 (1996)
  11. J.W.Fickett, C.S.Tung ” Assessment of protein coding measures” Nucl. Acid Res., 20, 6441 (1992.)
  12. D.Benton “Bioinformatics – principles and potential of a new multidisciplinary tool” Trends in Biotechnology, 14, 261 (1996)
  13. S.Kullback “Information theory and statistics” London, UK: John Wiley & Sons, Inc. Press. (1959)