A PROBABLE MUTUAL RELATIONSHIP BETWEEN LATENT PERIODIC GENE STRUCTURE AND PERIODIC CONFORMATION OF THE PROTEIN

CHALEY M.B.⁺, KOROTKOV E.V.

Centre “Bioengineering”, Russian Academy of Sciences, Prospect 60-letiya Oktyabrya, 7/1, Moscow, 117312, Russia;

e-mail: chaley@biengi.msk.su, chaley@biengi.ac.ru

+Corresponding author

Keywords: gene structure, periodicity, mutual information, Monte-Carlo simulation, protein conformation

A method for revealing latent periodicity of the nucleotide sequences [1] has been considerably modified in a case of small samples. This modified method has been used to look for the latent periodicity in the sequences of the EMBL data bank. A few examples of genes where a search of the latent periodicity has led to known periodic structures have been discussed in proof a reliability of the method.

A comparison of the artificial periodic sequences with a nucleotide sequence was used to reveal the latent periodicity of the later, as it has been reported earlier [1, 2]. An alphabet of the artificial sequences was consisted of S(i) letters, here i=1, …, n. In general, to reveal a period of n bases long a sequence S(1)S(2)…S(n)S(1)S(2)…S(n)S(1)S(2)…S(n)… was used. A length of the artificial sequence was chosen to be equal to the length of analysed nucleotide sequence. The artificial sequences having periods of 2, 3, …, n letters were compared in turn with analysed sequence. An each comparing resulted in filling up a matrix M(4,n). An element M(i,j) of the matrix showed a quantity of nucleotides of i-kind (i=A, T, C, G) which stood opposite a letter S(j) on the artificial sequence. The double mutual information value 2I was chosen as a measure of similarity, and it was counted proceeding from M(4,n) matrix [1, 2]. An independent varying of both left and right boarders of the artificial sequence together with DNA sequence was used for the search of periodicity region whose total length was unknown before. Though this method has been earlier described [1, 2], its application was impossible in a case of small samples, that is when a value of any M(i,j) element is less than 5. Then the double mutual information value 2I varies from  ² distribution, and one cannot appreciate precisely a probability of that the latent periodicity arose by accident. Such a situation usually occurs, if an analysed sequence is less long then 20n bases, here n is a period’s length.

A Monte Carlo method [3] has been used to take into consideration the influence of small samples. The method generated casual matrixes M(4,n) which had the same sum over columns

(1)

and over rows

(2)

as matrix M(4,n).

It was more convenient to make use of a value

(3)

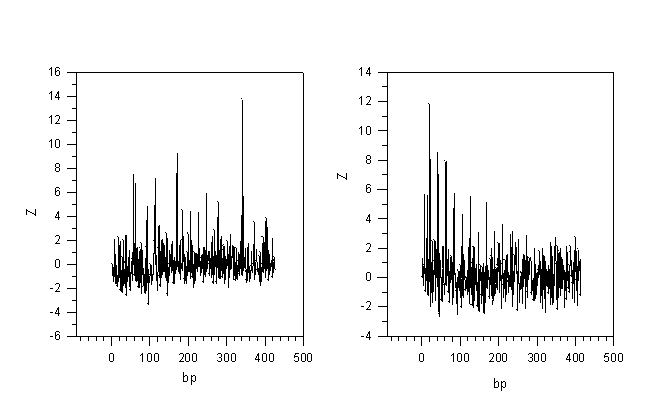
as a measure of accident led to appearance of periodic structure on nucleotide sequence. I’_m was a mean value of the mutual information I’ over the set of M’ matrixes, and s was equal to a square root of dispersion of the I’ value over the set. According to conducted estimations Z value equalled to 5 was correspond to the accidental probability of no more than 10^-6. The values of Z grater than 5 were correspond to the more less probability. A spectrum of Z values for all possible period’s lengths n was determined in the result of the calculations. Maximum period’s length was equal to one half of the full length of an analysed sequence. This allowed to reveal not only the latent periodicity but all possible duplications inside of a nucleotide sequence, also. The examples of Z spectra are shown in Figures 1,2.

The latent periodicity in separate genes permits to suppose that these genes have probably arisen by numerous duplications of some DNA fragment (see Fig.1, for example). At present time copies of such a fragment are so far eroded that no homology may be revealed between them. However, a periodicity existed at the level of nucleotide sequence is still retained on primary amino acid sequence or is traced in spatial protein organisation. Periodic spatial organisation of protein might also influence a formation of gene’s latent periodicity. We believe that gene structure being interrelated with protein structure may provide a key both to conformational interaction of proteins between themselves and to formation of their structural complexes. Proteins having the same kind of genes’ periodicity, probably, function in a similar fashion.

The same latent periodicity of 21 bases in genes of various bacterial chemoreceptors (see Fig. 2) is strengthening the supposition about a relationship between the latent periodicity of gene and structural peculiarities of its encoded protein and, furthermore, protein’s function. For analysed chemoreceptors it may be noticed that the latent periodicity of 21 bases was as a rule revealed in that region of the gene which was correspond to the second transmembrane and cytoplasmic domains. Such an identical periodic structure of chemoreceptors’ genes is more probable to be uncasual, and it is conditioned by the same mechanism of transduction of the signal of binding with ligand at a membrane surface into cytoplasm. But it is natural that membrane spanning domain binding a ligand has to show more structural variability.

References

1. E.V. Korotkov and M.A. Korotkova, “Latent periodicity of some human gene DNA sequences” DNA Seq. 5, 353 (1995)
2. E.V. Korotkov, M.A. Korotkova and J.S. Tulko, “Latent sequence periodicity of some oncogenes and DNA-binding protein genes” CABIOS 13, 37 (1997)
3. D.A Roff. and P. Bentzen, “The statistical analysis of Mitochondrial DNA polymorphisms:  ²and the problem of small samples” Mol. Biol. Evol. 6, 539 (1989)