SELECTIVE MODELS FOR MAPPING OF GENES IDENTIFIED IN RADIATION HYBRIDS

SVISCHEVA G.R.

Institute of Cytology and Genetics, Siberian Branch of Russian Academy of Sciences,   10 Lavrentiev Ave, 630090, Novosibirsk, Russia;
e-mail: aks@bionet.nsc.ru

Keywords: mammalian chromosomes, gene mapping, radiation hybrids, selective model

Abstract

A new type of selective models expanding the potentials of existing methods for radiation hybrid mapping of mammalian chromosomes is developed. It is designed for mapping of a combined set of genes identified in a clone either by direct molecular-genetic methods or by isozyme analysis. The selected gene included in the mapped group of genes can be strongly or weakly selected gene. Our models take into consideration the data on many genes simultaneously and allow one to use the partial information on RH clones. Asymptotic properties of new type of models are investigated. It is shown that models have psevdo-Markovian and additive properties and can be employed for mapping of an arbitrary number of genes. Estimates of a minimum number of localised genes for various models are obtained.

1. Introduction

Radiation hybrid mapping (RH), a somatic cell technique, was developed as a general approach for constructing long-range maps of mammalian chromosomes. This method suggested by Goss and Harris [1-4] is based on the ability of ionising radiation to induce chromosome breaks and leads to various chromosome rearrangements.

The process of obtaining haploid radiation hybrids begins with the irradiation of somatic cell hybrids containing a single human chromosome in a set of rodent chromosomes. The irradiation breaks chromosomes into pieces and kills the cells. The lethally irradiated cells are fused with normal non-irradiated rodent cell line. To simplify this process and make it less time-consuming a selective medium sorting out non-fused rodent cells was suggested. The inclusion of a selected gene in mapped gene group will ensure the presence of a unique set of fragments of the original human chromosome in each hybrid clone. Thus, each clone can be analysed for the presence or absence of particular human genes.

The statistical approaches for RH mapping allow one to determine the linear order of genes on the chromosome and estimate relative distances between them using the frequencies of various hybrid clones as experimental material.

The models simulating the biological process of obtaining clones are based on the common assumptions:

  1. the radiation-induced breaks along each chromosome occur at random and so may be modelled using a Poisson distribution;
  2. the fragments are retained and lost independently in RH clones;
  3. the more the distance between two linked genes, the more the probability of breaks between them.

Recently, with the development and wide use of DNA probes, a series of models for mapping DNA markers have been developed. These models permit one to map many genes simultaneously [5-9], including information on partially tested RH clones, and analyse haploid, diploid and polyploid clones. Bellow, I will speak on two most widespread selective models proposed by Lunnetta et al [10].

In a number of cases (for example, in analysis of mammals poorly studied genetically) isozymes are widely used for identification of a gene in a clone. The presence or absence of a gene is confirmed by its protein product. In this case it is impossible to use models for the ordering DNA markers due to possible loss of functions of an isozyme marker, caused by gene mutations. This leads to a false conclusion on absence of a gene. This fact is taken into account in the model of Ginsburg et al. [11-12]. by introducing the probability of the loss of gene functions. But this model has certain limitations. It is created for the analysis of four genes and excludes non-selective retention of fragments.

2. Models and their parameters

We offer a new class of selective models, designed for mapping of a combined set of genes identified by direct molecular-genetic methods or by isozyme analysis. The selected gene included in the mapped gene group can be strongly or weakly selected gene. In the case of stringent selection, only the hybrids with a selected gene are retained. Our models are designed for the analysis of RH clones containing a single copy of a chromosome of interest. Each of the models is represented by a joint distribution of probabilities of the observations of the genes in RH clones.

Let genes A1, A2, …, AL be identified in radiation hybrids. In a general case for the description of these models, it is necessary to introduce three types of parameters { i}, {rij} and { i}:

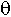  1.  i – the probability of at least one break between loci Ai and Ai+1 (1<= i<L), the number of such parameters is Nq = L-1;
  2. rij – the probability that a fragment containing a continuous sequence of loci from Ai to Aj is retained in the RH clone, the number of such parameters is Nr=L(L+1)/2;
  3.  i – the probability of loss of functions of the gene Ai, the number of such parameters is N=L.

The -parameters are of particular interest for geneticists. The r- and  -parameters are auxiliary. Npar=N+Nr+N=(L-1)+L(L+1)/2+L is the total number of parameters. If L is large, then abundant experimental data are required to estimate these parameters. Therefore, it is necessary to introduce certain limitations on auxiliary model parameters.

We shall consider three selective models that differ in restrictions on parameters {rij}. The S1 model assumes that the probabilities of retention of a fragments with a selected gene are equal to rs, and r for the others. In the S2 model, the differentiation of fragments without a selected gene is introduced: fragments located to the right of the selected gene are retained with probability rR, and the others are with probability rL. Such model formalisation permits one to consider the influence of a centromere and telomeres on the fragment retention [10]. We can see that the S1 model is a special case of the S2 model under the condition that r=rL=rR. Another special case of the S2 model is model S3 excluding non-selective retention of fragments (rL=rR=0). In the models, we assume that the probabilities of gene function loss are equal to d for all genes determined by isozyme analysis. For DNA markers, i=0.

Note that our S1 and S2 models develop existing selective models of Lunetta et al. [10] due to the introduction of probability of gene function loss. The S3 model updates the model of Ginsburg et al. [11-12]. Its difference from the above mentioned model is as follows: we do not consider possible deletion of gene and its subsequent retention as an individual fragment in a clone. We consider this event highly improbable.

3. Joint distribution of probabilities of genes in RH clones

The results of the analysis of each RH clone can be presented as an observation vector of genes x=(x1, x2,…, xL), where xi=1, if gene Ai was tested and retained, xi=0, if gene Ai was tested and not retained, and xi=?, if gene Ai was not tested in a given clone. We shall introduce the following designations to write a joint distribution of probabilities of observations of genes L P(x1, x2,…, xL) in RH clones.

Let the gene order be as follows A1, A2,…, AL. We shall designate chromosome breakage vector as b= (b1, b2,…, bL-1), where bi=1 if there is at least one break between adjacent genes Ai and Ai+1 (1<= i<L), otherwise bi=0. Then n(b)=b1+b2+…+bL-1 is the number of chromosome breaks, and (n(b)+1) is the number of fragments formed. We shall introduce M(b) as the ordered list of indices of terminal genes for the fragments:

The probability of a clone x=(x1, x2,…, xL) is expressed as 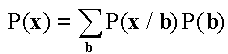, where

(1).

 

Here  i=1 if none of the genes located on fragment i was tested;

, if none of the tested genes on fragment i was retained; , if at least one tested gene of fragment i was retained in RH clone.

A joint distribution of probabilities of clones is calculated for each of the possible gene orders.

4. Properties of selective models

Our general model has no additive property expressed as:

However, the models S1, S2 and S3 exhibit additive property. But, these models are not Markovian. For all the models, we have shown that probabilities of only those clones are Markovian, in which all tested genes were retained.

It is easy to demonstrate that the probability of any observed clones may be expressed through marginal probabilities. In the current work, marginal probability is the probability of clones in which various number of genes was tested, and all of them are retained. As far as marginal probabilities have the Markovian property, the models S1, S2 and S3 may be called as pseudo-Markovian ones, and they are applicable for mapping of an arbitrary number of genes.

5. Determination of number of sufficient variables

All marginal probabilities can be expressed through probabilities which fix the presence of one or two tested genes. These probabilities can be presented in the form of a symmetric matrix. Thus, in order to obtain a joint distribution of probabilities of gene observations in clones completely, it is sufficient to determine the respective probabilities. We shall use a term “sufficient variable” for such probabilities. The number of sufficient variables W depends on selection type (weak or stringent). Under weak selection, W is equal to the total number of marginal probabilities where one or two genes are found: W=L(L+1)/2. Under stringent selection, W depends on location of a selected gene. W is equal to W=L(L+1)/2-LLLR or W=LR(LR+1)/2+LL(LL+1)/2, where LR is the number of genes to the right and LL – to the left of the selected gene, LR+LL+1=L.

6. Estimates of minimum number of genes for selective models

To estimate relative distances between genes, the maximum likelihood approach (dh) is commonly used. This method is based on solution of the system of equations: { dh/d pi=0, i=1, Npar}, where dh/d pi is the first partial derivative of the likelihood function with respect to estimated parameter. If Npar is greater than the number of sufficient variables W, we can’t estimate each of the parameters, since only W equations are independent. The condition (Npar <=W) is fulfilled under weak selection starting with L=3. In the case of stringent selection the situation depends on the location of a selected gene. W reaches minimum, when selected gene is central (s=[(L+1)/2], square brackets denote an integer of a number). W reaches maximum, when selected gene is terminal (s=1 or s=L). Under stringent selection, the condition essential for estimating all model parameters is fulfilled starting with L=4 for the S3 model, with L=5 – for the S1 model and with L=6 – for the S2 model.

It should be emphasised that the problem of mapping of a small number of genes (L=3,4,5) under stringent selection is not completely solved, since it is impossible to estimate relative distances between genes without introducing additional restrictions on the parameters. However, due to introducing these restrictions, the model may not to reflect real situation, and eventually results in the false determination of gene order. This problem exists for all selective models, and not just for the models offered by us.

Acknowledgements

The author expresses gratitude to Ginsburg E. Kh. for initiation of this work, Axenovich T. I. and Yudanin A. Y. for the help and valuable advises.

References

  1. Goss S. J., Harris H., “New method for mapping genes in human chromosomes” Nature. 1975. V. 225. P. 680-684.
  2. Goss S. J., Harris H., “Gene transfer by means of cell fusion. I. Statistical mapping of the human X-chromosome by analysis radiation-induced gene segregation” J. Cell Sci. 1977. V. 25. P. 17-37.
  3. Goss S. J., Harris H., “Gene transfer by means of cell fusion. II. The mapping of 8 loci on human chromosome 1 by statistical analysis of gene assortment in somatic cell hybrids” J. Cell Sci. 1977. V. 25. P. 39-57.
  4. Goss S.J., “Radiation-induced segregation of synthetic loci: a new approach to human gene mapping” Cytogenet. Cell Genet. 1976. V. 16. P. 138-141.
  5. Boehnke M., Lange K., Cox D. R., “Statistical methods for multipoint radiation mapping” Am. J. Hum. Genet. 1991. V. 49. P. 1174-1188.
  6. Bishop D. T., Crockford G. P., “Comparisons of radiation hybrid mapping and linkage mapping” Cytogenet. Cell Genet. 1992. V. 59. P. 93-95.
  7. Boehnke M., “Radiation hybrid mapping by minimisation of the number of obligate chromosome breaks” Cytogenet. Cell Genet. 1992. V. 59. P. 96-98.
  8. Chakravarti A., Reefer J. E., “A theory for radiation hybrid (Goss-Harris) mapping: application to proximal 21 q markers” Cytogenet. Cell Genet. 1992. V. 59. P. 99-101.
  9. Green P., “Construction and comparison of chromosome 21 radiation hybrid and linkage maps using CRI-MAP” Cytogenet. Cell Genet. 1992. V. 59. P. 122-124.
  10. Lunetta K., Boehnke M., Lange K., Cox D., “Selective locus and multiple panel models for radiation hybrid mapping” Am. J. Hum. Genet. 1996. V.59. P. 71-725.
  11. Ginsburg E. Kh., Svischeva G. R., Yudanin A. Y., Nesterova T. B., Zakian S. M., “Statistical treatment of radiation mapping experiments” Genetika (Russia). 1993. O. 29. N 11. C. 1921-1932.
  12. Nesterova T. B., Mazurok N. A., Matveeva N. M., Shilov A. G., Yantsen E. I., Ginsburg E. Kh., Goss S. J., Zakian S. M., “Demonstration of the X-linkege and order of the genes GLA, G6PD, HPRT, and PGK in two vole species of the genus Microtus” Cytogenet. and Cell Genet. 1994. V. 65. P. 250-255.