BUGAENKO N.N.+, GORBAN A.N., SAPOZHNIKOV A.N.
Institute of Computational Modeling of, Siberian Branch of the Russian Academy of Sciences, Akademgorodok, Krasnoyarsk-36, 660036, Russia;
e-mail: bugar@cc.krascience.rssi.ru
+Corresponding author
Keywords: symbolic chain, symbol composition, information, entropy, frequency dictionary, binary classification
Abstract
A method of classification of symbols in symbol chain (text) for revealing differences of statistical characteristics of real and random texts with the same symbol composition is proposed. The method is based on maximization of a function representing information containing in one text (its frequency dictionary) with respect to other. Several methods of approximate solutions are proposed. Introduced earlier by authors limit entropy is used as a control statistical quantity in checking up the obtained classifications. Performed experiments with construction of binary classifications show effectiveness of the method.
1. Introduction
The presence of regularities in a text can be understood as its difference from a random text – obtained by random rearrangement of elementary units of the initial text. Obviously, such a definition strongly depends on definition of elementary units. In the present paper we assume that this problem is already solved, and the elementary units are determined and denoted by different symbols. Here the next obstacle arises: the problem of finiteness of the text being analyzed. If the number N of different elementary units in the text is such that N2 is close to the length of the text or exceeds it, then it is impossible even to analyze the statistics of pairs. One must introduce new alphabets, combining ‘categories’ and ‘classes’ of units and denoting them by the same symbol. The question is: how to do that in the best way?
As a primary object we considered the sequences of amino acids in peptides. The accepted point of view is that the sequence of amino acids in peptide is random or ‘almost random’. Randomness is understood as similarity of the initial aminoacid sequence and those obtained from it by random rearrangement of its elements. At that, the amino acid sequence is considered as a text, i.e. as a sequence of symbols, each of them denoting one aminoacid of the same kind. One of the first difficulties in statistical analysis of such texts – too large alphabet under comparably short length of the text. So, for example, there are 400 two-pair combinations, and in order to make a reasonable statistics for them one should have a considerably longer text. Such texts are not so numerous, and analysis of three-pair combinations for aminoacid sequences under usual approach is impossible at all (in contrast to nucleic acids with 4-letter alphabet). The solution is searched for in diverse classifications of aminoacids, constructed in accordance with physical or chemical properties of those. The aminoacids belonging to one class are denoted by one symbol. So, the number of symbols in alphabet decreases and a possibility appears to make statistical analysis of the succession of amino acids in real peptide. There are works demonstrating that the characteristics of succession of amino acids in real peptide cannot be distinguished from those in randomly rearranged sequences for diverse classifications of amino acids.
2. General approach
Earlier [1], we introduced an approach to consideration of symbol chains in terms of frequency dictionaries. Frequency dictionary of the length q of a chain is obtained when a frame of reading of the length q moves along the chain shifting one symbol per step. The frame of reading reads words of the length q. The frequency dictionary of the length q is the set of the words and their frequencies (how often they are encountered in the text). Starting from the maximum entropy principle, we have obtained formulas for reconstruction of larger dictionaries from shorter ones; but, what is important here, we have introduced the notion of limit entropy of dictionary of length q 
, which is
for q>1, and 
for q=1,
where Sq is Shannon entropy of the dictionary, and M is the dimension of the text alphabet. It has been shown that the limit entropy characterizes information content of each dictionary.
Thus, for revealing regularities the following task should be solved: to construct such a classification of symbols that for it the limit entropy of the dictionary (of some predetermined length q) be maximally different from average limit entropy of dictionaries of the length q of corresponding (with the same symbol composition) random texts.
As a measure of deviation of certain distribution 
from its equilibrium values 
can be taken convex function 
, which is one of definitions of additional information (“negative entropy”) containing in with respect to 
(see, for example, [2]). The function 
is non-negative and turns into zero if and only if for all i 
=
.
The frequencies 
of words of the length q are determined by direct calculations. The average frequencies 
of words of length q for randomly rearranged texts are expressed from the frequencies of individual symbols (dictionary of the length 1) as 
. Then the information of real dictionary of the length q with respect to random dictionary is determined as
.
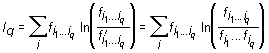So, if we want that in some classification the information content of the dictionary of the length q of a given text would be maximally different from information content of dictionaries of the length q of random texts, the classification (redesignation of several different symbols by one symbol) should be done so that the frequencies 
and 
,…, 
of the dictionaries of the length q and 1 of the text rewritten in new denotations would ensure maximum of corresponding function 
:
.
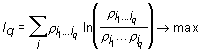3. Solutions
Exact solution can be obtained by complete look through. Suboptimal classifications can be obtained, for example, by numerical methods: turning to continuous functions, one can determine the point of maximum of moving along the gradient, and then return to the discrete case, moving from the obtained point to the nearest discrete knot where the function is maximal. The solution by complete look through demands for unacceptable amount of calculations in general case.
An approximate method of solution, which does not demand for full look through the variants but also does not guarantees coming to the global maximum is to ‘glue’ by two or three symbols ascribing them to one class, then look through the complete set of such ‘gluings’, choose the best and try to continue ‘to glue’ until coming to local maximum of .
This is the way of classification ‘from above’. The another variant of the same method is classification ‘from below’, when at the beginning all the symbols are ascribed to one class, and then one tries to increase the number of classes, transferring in a new class by one or two symbols, fixing the best obtained at this step classification and starting again from it. We can expect that if on the way ‘from above’ we come to the same point as on the way ‘from below’, that is the point of global maximum.
It should be stressed that the above methods can be applied not only to single symbol chain, but to a group of chains to obtain common classification revealing common peculiarities of all chains together.
4. Results
For testing of the proposed method we have constructed binary (division into two classes) classifications for several groups of peptides, several hundreds of peptides in each group. A number of experiments has been performed with single chains. For each group (and single chain) we constructed three classifications so that to obtain maximal differences of random and real dictionaries at the lengths q=2, 3 and 4. We give here general results:
- the use of limit entropy as a characteristic of information content of dictionaries allows to determine the difference of real and random texts for diverse dictionary lengths and diverse classifications;
- the proposed method of construction of classifications on the basis of maximization of information content of dictionary of given length of real text with respect to dictionaries of random texts allows to obtain reliable differences of limit entropies of real and random texts both for groups of chains and for single chains;
- for the given sequence of symbols always exists a classification revealing the difference from random chains.
Biophysical interpretation of the obtained classifications will be made after careful consideration.
Acknowledgements
This work was partly supported by the Krasnoyarsk Regional Science Foundation (grant 7F0012).
References
- Bugaenko, N.N., Gorban, A.N. and Sadovsky, M.G.: Information content in nucleotide sequences. Molecular Biology. 30(3), Part 1, (1996), 313-320.
- Gorban, A.N. Equilibrium encircling. Novisibirsk: Nauka, 1984. 256 p.