MAXIMUM ENTROPY PRINCIPLE AND MEASUREMENT OF INFORMATION CONTENT OF GENETIC TEXT

BUGAENKO N.N.+, GORBAN A.N., SADOVSKY M.G.1

Institute of Computational Modeling of Siberian Branch of the Russian Academy of Sciences,

1Institute of Biophysics of Siberian Branch of the Russian Academy of Sciences, Akademgorodok, Krasnoyarsk-36, 660036, Russia;
e-mail: bugar@cc.krascience.rssi.ru;

+Corresponding author

Keywords: nucleotide sequence, genetic text, frequency dictionary, entropy, random sequences

The information capacity in frequency dictionaries of nucleotide sequences is estimated through the accuracy of reconstruction of a longer frequency dictionary from a short one. This reconstruction is performed by the maximum entropy method. Real nucleotide sequences are compared to the random ones. Phages genes from NCBI bank were analyzed. The reliable difference of real genetic texts from the random sequences is observed for the dictionary’s length q = 2, 5 and 6.

1. Introduction

Application of mathematical methods for studying nucleotide sequences is a long-standing story. At present, the variety of methods developed can be divided into two classes: methods involving context and context-free analysis of symbolic (nucleotide, in particular) sequences. The context-involving methods assume special biological knowledge and aim both the analysis of groups of nucleotide sequences to obtain statistical characteristics and consideration of single sequences to recognize functional sites, introns, exons etc. Being more abstract, the context-free methods are assumed to avoid any involving of the knowledge of this sort; mainly, they take origin from methodology of statistical physics. The study of statistical properties of nucleotide sequences means a transition from the consideration of specific nucleotide sequence to the consideration of ensembles of their fragments [1-4].

2. Reading window and frequency dictionary

Here we present the methodology of investigating the DNA primary structure as a text. DNA or RNA nucleotide sequence is considered as a linear connected sequence of symbols and is called genetic text (GT), the number N of symbols in the text is called the length of GT.

All known intracellular processes related to realization of genetic information involve different fragments of DNA (or RNA) not greatly varying in length. The information is read locally, by small portions and from small DNA regions. During the information processing, the reading “device” runs along the nucleotide sequence in small steps. Let us call such a device the reading window. Let assume that 1) the read fragment is of a permanent length, 2) the reading window moves permanently in the same direction, and 3) the step of the reading window motion is permanent and equals to one nucleotide. A site of DNA (or RNA) read by the reading window of the length q would be called a word of the length q. Complete set of the words encountered in GT, accomplished by their frequencies is called Frequency Dictionary (FD) [5–8].

3. Dictionary reconstruction. Maximum entropy method

The shorter dictionary could be always obtained from the given one by summation of frequencies of the words; the inverse transition, in general case, is impossible. We call the problem of longer dictionary derivation from given one the problem of dictionary reconstruction. We solve this problem by the maximum entropy method, that implies using the information contained in the given dictionary only and avoiding an involvement of any external knowledge.

Let reconstruct a longer dictionary from the given one so that the reconstructed dictionary showed the maximal indeterminacy. That means that one must choose the longer dictionary with maximal entropy, which we define in traditional way:

(1)

where ij is a letter (symbol) from the text alphabet; i1…iq represents a word of the length q. ij runs the letters {A, C, G, T} in our case.  is the frequency of word. The summation here is performed over all the words encountered in the text. In order to eliminate boundary effects, we close a texts studied into a ring.

Solving the extremum problem

(2)

under the condition of interconnectedness of the given and longer dictionaries, we obtain

, q> 1 and , q = 1

(3)

The expressions (3) for the reconstructed frequencies are analogous to Kirkwood approximation [5, 6] in statistical physics, but unlike this latter, are the exact solutions.

4. Entropy, limit entropy, informativity and dictionary reconstruction quality

Let Si(j) be the entropy of dictionary of the length i reconstructed from a given dictionary of the length j (i > j) of. Formulas (1) and (3) yield

, j> 1 and

(4)

The entropies Si steadily increase with the dictionary length i, while the entropies Si(j) steadily decrease as j grows from 1 to i.

Let introduce the notion of informativity. The maximal possible entropy for a dictionary of length i is

4i is the maximal possible number of words in a dictionary of length i. Then the informativity should be introduced as

(5)

Zero informativity corresponds to a dictionary with complete set of words of equal frequencies. As opposed to entropy, this characteristic is a measure of deviation from disorder.

Due to Ii, one can compare the dictionaries of equal lengths of different sequences over their indeterminacy. In order to compare the dictionaries of different lengths, we introduce the notion of limit specific entropy. Reconstruct a dictionary of the length n from a given dictionary of smaller length j and consider the limit Sn(j)/n as n ®  ? . It corresponds to the well-known thermodynamical limit in statistical physics.

(6)

 

For the dictionary of the length j = 1 we have

(7)

This is the specific entropy (entropy per a symbol) in a dictionary of infinitely long words, reconstituted from the given dictionary. Further on we omit the word “specific,” since we will not mean the true limit (infinite) entropy. Since max(S1) = ln4, let define the limit entropy as

, j > 1 and ; j = 1

(8)

It varies from zero (complete determinacy) to one (complete indeterminacy). The entropy difference between two dictionaries of two consecutive lengths yields the information gain of longer dictionary.

Also introduce informativity of a dictionary of length i reconstructed from a dictionary of length j

(9)

Two dictionaries with the same entropy but of different lengths have different informativities (the informativity is higher for a longer dictionary). Equal entropies indicate a similar indeterminacy of choosing a word of given length in an arbitrary text site, while unequal informativities indicate that the longer dictionary is more exotic.

Let compare informativities of the real and reconstructed dictionaries. We call  the quality of reconstruction of dictionary of the length i from dictionary of the length j < i:

(10)

 

Since Si(j) >= Si, the quality of reconstruction varies within 0 <=  <= 1, where unity corresponds to the case Si(j) = Si, which is the case of exact reconstruction.

5. Comparison of real and random texts

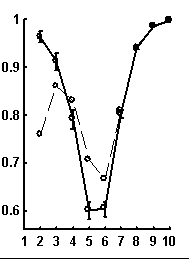
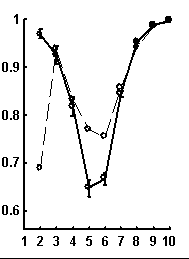
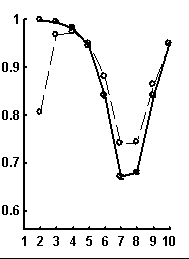
Let call a random text corresponding to the given real text a text obtained by random rearrangement if its elements. We have considered a number of texts of nucleotide sequences from NCBI server. The dictionaries of the lengths from 1 to 10 were constructed for each text and the limit entropies and qualities of reconstruction were calculated. Besides, 100 random texts have been constructed for each real sequence, and the average values and standard devi-ations of those were calculated. In general, the patterns seem to be rather similar for sequences of different organisms. Typical values for qualities of reconstruction are shown in Fig. 1.

 

a) b) c)

 

Length of reconstructed dictionary

Figure. 1. Examples of the dependence of quality of reconstruction of dictionary of (q + 1)-length derived from dictionary of the length q; the length of reconstructed dictionary is represented on horizontal axis. a) a sequence from chicken genome, N=2136; b) a sequence from human genome, N=1639; c) a sequence from nematoda genome, N=26139. Dashed line connects the quality of reconstruction for real sequences, while solid line connects that latter for random noncorrelated sequences of the same nucleotide composition. The standard deviations are shown.

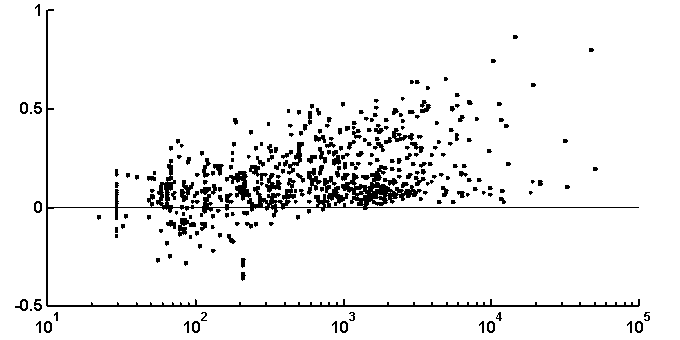
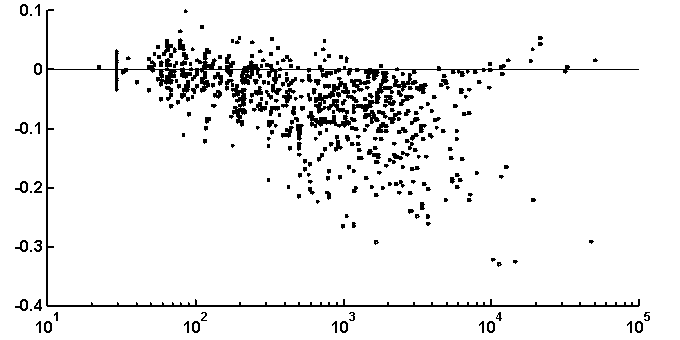
It is peculiar that the dictionary of the length 2 is badly reconstructed from the unit dictionary for real nucleotide sequences, while  is similar for real and random texts. That means, that the dictionary of real texts of the length 2 contains an essential part of information about the dictionary of the length 3. The dictionaries of the lengths 5 and 6 being reconstructed from one symbol shorter dictionaries are better for the real sequences in comparison to the random ones. To demonstrate the generality of these effects and observe entire picture, we have analyzed over 1000 phages genes. The results of calculation of quality of reconstruction for that group of genes are shown in Fig. 2. One can see that brightly revealing peculiarities are observed only for the texts long enough, as a rule of more than 500 nucleotides. The effect of finiteness impacts greatly for shorter texts.

 

a) b)
c)

 

6. Discussion

An explicit formula for the approximate reconstruction of the longer dictionaries from the shorter ones is obtained; this formula has a maximal generality and does not imply (explicitly or implicitly) any special assumptions on the properties of original nucleotide sequences, or their models. Our formula implies all known approximate methods of statistical investigation of nucleotide sequences based on modelling of them by Markov chains of various orders.

The approach presented above is illustrated with calculations implemented over a number various real genes. Below are described the results of analysis of all the phage sequences obtained from NCBI databank (release 94). The comparison of real and random genetic texts shows that:

  • the dictionaries of the length two of real and random sequences possess reliably different information capacity;
  • the dictionary of the length two of real genetic text bears reliably more information about the whole text in comparison to the dictionaries of the length two of random texts;
  • the increase of information content in dictionaries of the length three when compared to dictionaries of length two is reliably smaller for the real texts than for random ones;
  • the dictionary of the length eight bears over 90% of total information about the genetic text.

Acknowledgements

This work was partly supported by the Krasnoyarsk Regional Science Foundation (grant 7F0012).

References

  1. Brendel, V., Beckmann, J.S. and Trifonov, E.N.: Linguistics of nucleotide sequences: morphology and comparison of vocabularies, J. Biomol. Struct. Dyn. 4 (1986), 11-22.
  2. Pevzner, P.A., Borodovski, M.Yu. and Mironov, A.A.: 1. The significance of deviation from mean statistical characteristics and prediction of the frequency of occurences of words, J. Biomol. Struct. Dyn. 6 (1989), 1013-1026.
  3. Martingale, C. and Konopka, A.K.: Oligonucleotide frequencies in DNA follow a Yule distribution, Computers and Chemistry. 20(1) (1996), 45 – 38.
  4. Mirkes, E.M., Popova, T.G. and Sadovsky, M.G.: Investigating statistical properties of genetic texts: a new approach, Adv. in Modelling and Analysis, ser. B. 27 (1993), 1–13.
  5. Kirkwood, J. and Boggs, E.: The radial distribution function in liquids, J.Chem.Phys. 10(6) (1942), 394.
  6. Bugaenko, N.N., Gorban A.N. and Karlin, I.V.: Universal expansion of three-particle distribution function, Teoret. i mat. fizika. 88(3) (1991), 430-441. (English translation: Theoretical and Mathematical physics. (1992) 977-985 (Plenum Publ. Corp)).
  7. Popova, T.G. and Sadovsky, M.G.: The new measure of relationship between two symbolic sequences, Advances in Modelling & Analysis, ser. A. 22(2) (1994), 13–17.
  8. Mirkes, E.M., Popova, T.G. and Sadovsky, M.G.: Investigating statistical properties of genetic texts: a new approach, Advances in Modelling & Analysis, ser. B. 27(1) (1993), 11–13.
  9. Popova, T.G. and Sadovsky, M.G.: Investigating statistical properties of genetic texts: new method to compare two genes, Modelling, Measurement & Control, ser. C. 45(4) (1994), 27–36.
  10. Bugaenko, N.N., Gorban, A.N. and Sadovsky, M.G.: Information content in nucleotide sequences. Molecular Biology. 30(3), Part 1, (1996), 313-320.