Institute of Cytology and Genetics, Siberian Branch of the Russian Academy of Sciences, 10 Lavrentiev Ave., Novosibirsk, 630090, Russia;
e-mail: titov@bionet.nsc.ru
Keywords: double helix, and RNA secondary structure, statistical thermodynamics, Ising model
Abstract
Methods of statistical thermodynamics were used to develop the model of the growth of double helix of nucleic acids of uniform composition. The growing double helix was considered as a quasi equilibrium dynamic structure where the monomers can quickly pass into a less thremodynamically favored conformation. Statistics of these conformations is described within the frames of an Ising-type model. It is shown that behavior of the free energy of the system depending on the growing helix length can be nonmonotonic: the length with the maximal free energy represents the critical nucleus size. Applications of the model to interpretation of experimental data and RNA secondary structure analysis are discussed.
1. Introduction
Double helix formation is a three-stage process [1-3] comprising i) bringing the strands into spatial proximity, ii) forming the critical nucleus, and iii) quick “zippering” of the helix (Fig. 1). The concept of critical nucleus several base pairs long was introduced phenomenologically [2] to interpret the apparent negative activation energies for association rates of complementary oligonucleotides. In this paper we develop a microscopic model of critical nucleus.
Figure 1. Kinetic scheme of double helix formation.
Double helix of nucleic acids is a dynamic structure with motions occurring on different time scales. At an appropriate time scale, the faster degrees of freedom of the system may be regarded as internal and the equilibrium between them as being reached. In this work, we study the helix growth using thermodynamic approach. The physical basis of the work rests on the analysis of the process at intermediate times exceeding the times of structure relaxation within an individual base pair.
Constructing the partition function of a homogeneous duplex in an Ising-type model, we obtain its free energy as a function of the helix length composed of two terms opposite in sign: the gain from the helix elongation and the destabilization due to local structure fluctuations. The balance of these factors determines the length of the nucleus: the nucleation occurs barrier-free if the thermodynamic “force” of helix-coil transition exceeds the critical value. Application of the model to nucleation of the helices of nonuniform composition (in particular, to formation of RNA secondary structure) and extraction of nucleation parameters from the experiments under equilibrium conditions are discussed.
2. Theory
2.1. Partition function of a quasiequilibrium double helix
Let us consider the growth of a helix from two complementary strands, each consisted of N identical nucleotides. At each instant of time, the forming duplex consists of the growing helix and the regions of the strands not yet involved in the helix formation, the so-called “free ends”. If the states of the nucleotides in the helix and free ends are independent, the partition function Z of the duplex resolves into the product of their partition functions Z = Zcore(n) Zend(N-n).
Growth of the double helix is conventionally characterized by the elongation parameter [1], that is, the statistical weight s of the paired state of the nucleotide compared to its coiled state. Except for the very vicinity of the melting point, the formation of coiled regions within the helix can be neglected at the intermediate times. However, a quicker forming of helix “defects” is possible, that is, nucleotide transitions into conformations less thermodynamically favored but stabilized relative to the coiled state through interaction with the immediate environment. Similarly to the Zimm-Bregg’s model [1], we introduce additionally the elongation parameter s1 and cooperativity u to describe these states. Then, the helix transition operator is:
Q =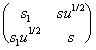 
Determination of the free ends transition operator allows us to calculate the partition functions Zcore(n) and Zend(N-n) through summing over the states of all the nucleotides. The free energy of the duplex is determined from the conventional thermodynamic identity Fn = – kT lnZ(n).
2.2. Model of critical nucleus
Using the above-described procedure, the equation expressing the free energy of the duplex can be reduced to a balance of two terms opposite in sign:
Fn /kT – F0 /kT = – n D – ln( + (1 – ) exp(- n / Nc)), |
(1) |
where the nondimensional parameters introduced are determined by the eigenvalues of transition operators and have the following meaning for the double-stranded polymer: (1) q is the equilibrium fraction of the base pairs occurring in the most favored conformation; (2) D characterizes the free energy gain obtained with the helix elongation by one base pair; and (3) Nc is a characteristic length where a single “defect” pair perturbs the state of the encompassing pairs.
The first term in expression (1) represents the decrease in the free energy caused by base pair addition; the second term arises from its increase with pertubation of the most stable helix structure. The character of dependence F(n) for different values of thermodynamic “force” of transition D changes from an increasing curve at the melting point of the double-stranded polymer (D = 0) to a descending straight line Fn = – nD corresponding the lack of the defects ( = 1). The character of the dependence changes at intermediate D values: when NcD < 1- , it is nonmonotonic with a metastable F(n) minimum at n = 0; when NcD > 1- , this minimum disappears and F(n) decreases monotonically.
The region of F(n) increase characterizes the helix pre-equilibrium; the critical nucleus size n is derived from condition of maximal free energy at the critical point:
n = Nc ln (  ) if NcD < 1- , n = 0 at NcD>1- |
(2) |
3. Discussion
3.1. Critical nucleus and activation energy of helix denaturation rate
Measuring the activation energy of renaturation rate of strands rAN +rUN, Porschke and Eigen [2] estimated the size of the nucleus n = 3-4 bp. Analysis of expression (1) at low temperatures demonstrates that the activation energy of helix denaturation (in this limit) can be approximated by the linear function of its length Ea = (N – n ) D H, where D H is the difference between the enthalpies of the single- and double-stranded ordered states. (In other words, the helix denaturation occurs activationally for the lengths exceeding that of the critical nucleus; when this length is reached, a spontaneous dissociation takes place.) According to this approximation, we performed a linear regression of their equilibrium data [2] involving denaturation enthalpies of duplexes rAN +rUN with variable N and obtained the average value of n = 3.2. Since renaturation activation energies are measured with considerable experimental error, analysis of the melting data is likely to provide a more precise estimation of the critical nucleus.
3.2. Critical nucleus and activation energy of helix association rate
Historically, the critical nucleus was postulated to explain large values (up to -17.5 kcal/mol [1]) of apparent negative activation energies of the association rate. The direct identification of the difference in free energy (1) with activation barrier predicts a smaller value of nucleation barrier (the maximal value of the difference Fn – F0 is equal to kT ln2). Note, however, that activation energy is determined by differentiation of the process rate with respect to temperature and, in doing so, the temperature dependence of critical nucleus size (2) could be important.
3.3. Formation of helices of nonuniform composition
Since the nucleation barrier depends essentially on the thermodynamic “force” of transition (compare with (1)), a predominant involvement of strong (G-C) pairs in the nucleation should be expected in the strands of nonuniform composition and, consequently, the linear increase in association rate with their concentration, independence of nucleation centers provided. (Such dependence is actually observed in DNA polymers [3].) Using the experimental data [1], we evaluated that the contribution of the strong and weak pairs to the association rate of ribooligonucleotides differs at 21-23 CА by almost two orders of magnitude: ks 
1.5-106 M-1s-1 and kw 5-104 M-1s-1 per one base pair, respectively.
3.4. Application to the computer-assisted prediction of RNA folding
The nucleation rate is considered independent of the nucleotide context in the available algorithms for simulation of RNA folding kinetics. We are planning to find out whether the consideration of the nucleation heterogeneity (3.3) will increase the RNA secondary structure prediction accuracy.
Note that the specific content of G-C pairs in the helices formed by the regions remote along the sequences in the phylogenetically proved secondary structure of 16S RNA is on the average higher than in the helices formed by short-range interactions [4, 5]. It is another point in favor of kinetic control over the folding of this molecule (the calculated free energy of its native secondary structure is considerably higher than the value minimally possible [6] according to the existing energy rules).
3.5. The length of “coherence” of conformational states of base pairs Nc is a fundamental parameter of “breathing” helix
The physical basis of our model of the critical nucleus is the fact [1, 2] that the double helix formation is a relatively slow process compared to the structure relaxation within an individual base pair and is controlled through the monomolecular stage of a stable region (critical nucleus) formation. Its typical length is determined by an intermediate spatial parameter, the defect correlation radius. The “fraying” of the base pairs at the ends of the helix has the same physical nature of the structural transitions and may be analyzed similarly. Coincidence of the typical nucleus length (2-4 base pairs) with the length of orientational correlations of base pairs in a fluctuating DNA [7] is likely to be nonaccidental too.
3.6. The movement of the double helix boundary, taking into account the conformational relaxation of its nucleus and single-stranded ends, can be considered as a one-dimensional diffusion with memory in a space of nucleus length
Although we don’t calculate the nucleation rate, since we don’t introduce a detailed kinetic scheme, there is possible to evaluate the critical nucleus length and to establish the physical reason for existence of previously postulated [2] metastable states. If the local deviations in the helix structure are taken into account, the state of the helix cannot be described by the number of the constituent bases alone, but is also determined by the number of these deviations and how they are distributed within the helix. Kinetic analysis in terms of diffusional problem on the first attainment [8] is a non-trivial task, since the diffusion in the medium with an additional thermodynamic variable (and there are two variables here: the subsystems of defects and free ends are relaxing independently) is non-Markovian.
Acknowledgements
The author is grateful to N.A. Kolchanov for his attention to the work. The work was supported by the grants INTAS-RFBR 95-0653 and RFBR 97-04-49740 and the Integration Program of the Siberian Branch of the Russian Academy of Sciences.
References
- C.R. Cantor and P.R. Schimmel, “Biophysical chemistry” (Freeman & C, San Francisco, 1980).
- D. Porschke and M.J. Eigen, “Cooperative non-enzymic base recognition. III. Kinetics of the helix-coil transition of the oligoribouridylic-oligoriboadenylic acid system and of the oligoriboadenylic acid alone at acidic pH” J. Mol. Biol. 62, 361 (1971).
- J.G. Wetmur and N.J. Davidson, “Kinetics of renaturation of DNA” J. Mol. Biol. 31, 349 (1968).
- T.A. Faizullin, “Non-equilibrium of RNA secondary structure” (Diploma Thesis, Novosibirsk State University, 1994).
- O.V. Galzitskaya “Effect of remote-contact energy on the time of attaining the native structure for RNA-like heteropolymers” Molek. Biol. 31, 488 (1997) (Russian).
- I.V. Hofacker et al., “Fast folding and comparison of RNA secondary structures” Mon. fur Chem. 125, 167 (1994).
- V.B. Zhurkin, “Local dynamics within the DNA double helix. Comparison of the conformational analysis with the experiment” Molek. Biol. 17, 622 (1983) (Russian).
- V.V. Anshelevich et al., “Slow relaxation processes in the melting of linear biopolymers: a theory and its application to nucleic acids” Biopolymers 23, 39 (1984).