ROYTBERG M.A.+, SEMIONENKOV M.N., TABOLINA O.Yu.
Institute of the Mathematical Problems in Biology, Pushchino, 142292, Russia;
e-mail: roytberg@impb.serpukhov.su
+Corresponding author
Keywords: amino acid sequences, alignment, weight matrix, computer experiment
The paper is devoted to the problem of how to choose a biologically correct alignment of two sequences at a given substitution weight matrix (cf. [1, 10, 11]).
The approach is based on the observation that the gaps in alignments of the independent random and the similar sequences play fundamentally different roles. In an alignment of two random sequences a gap introduced into one of them does not usually lead to a considerable increase of the number of matches. At the same time a correct gap in one of even marginally similar biological sequences can reconstruct a matching of rather long similar segments in the sequences and, therefore, the number of matches can increase substantially.
Consider two sequences u and v and fix a substitution weight matrix. For an arbitrary number of gaps g let S(g) be the maximum total weight of substitutions in alignments of the sequences u, v containing at most g gaps, and let D(g) be it’s ‘derivative’:
D(g) = S(g+1) – S(g)
Computer experiments with random and natural biological sequences show the following.
S1. Let u be a random sequence and a sequence v is obtained from u by random substitutions (without insertions/deletions). Then for all number of gaps g the value of S(g) increases slowly and D(g) is small.
S2. Let u be a random sequence and a sequence v is obtained from u by random substitutions and some insertions/deletions. Then initially the value of S(g) increases rather fast, i.e. the values of D(g) are large. After some value of g (hereafter called critical) the values of S(g) grows much more slowly, i.e. D(g) is small.
S3. Let u and v be amino acid sequences of homological proteins with known correct alignment (e.g. obtained from 3D-structures of the proteins). Then the behaviour of S(g) is analogous to the one of the above, the shape of S(g) being dependent on existence of gaps in the correct alignment (see Fig. 1).
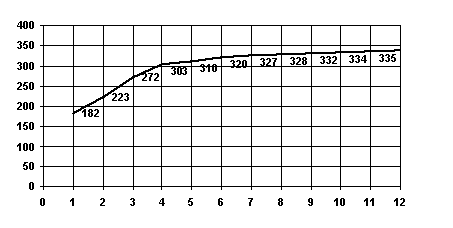
Figure 1. The maximal total weight S(g) of substitutions in alignments containing at most g gaps for the alpha- vs beta-chain of horse hemoglobin (PDB code 2mhb). The critical number of gaps is 4 and S(4) = 303. See also fig.2.
This property can clearly be interpreted as follows (see Fig.2). Suppose, that there exists a set of gaps for sequences u and v which leads to a correct alignment and each gap from this set establishes a correspondence between rather long fragments of the initial sequences and, thus, its correct positioning provides substantial increase in the total weight of substitutions of S(g). When all the correct gaps are introduced (this corresponds to the critical value of g), a new gap does not lead to a considerable increase in S(g). If there are no reasonable gaps, we came to case S1 In this case the critical value of g correspond to the left end of the plot.
Thus our approach to the sequence alignment is to find out an alignment providing the maximal substitution score among all alignments having critical number of gaps. We believe that the alignment is the biologically correct one. Note, that we don’t use any gap or deletion penalties. From other hand, the proposed approach can be treated as a way to find out a proper gap penalty function for given sequences.
For practical implementation of the approach one has to know what values of D(g) are significant for given pair of sequences. To obtain the threshold desired we have done computer experiments with random nucleotide and protein sequences related to one another as described in S1. We calculated the average values of the possible jumps D(g) for the different rates of similarity and different lengths of the sequences (see Fig. 3). When one knows the values of S(g) and D(g) the table presented allows to decide which values are “small” and thus to find the critical number of gaps g.
The approach is implemented as a C-program PAL. To find out the values of S(g) for the different number of gaps g the program uses an algorithm constructing a set of all so called Pareto-optimal alignments of two given sequences [R94]. Here we call an alignment Pareto-optimal if no other alignment has greater substitution score and smaller number of gaps simultaneously. The notion of Pareto-optimal alignment is dual to the concept of decomposition of the parametric space ([4, 11]). The algorithm is based on the proper modification of the dynamical programming (cf. [2, 3, 10]) and allows to support in the program various useful options, e.g. work with the sequences in the arbitrary alphabet, alignment of symbolic sequence with the profile ([7, 8]), implementation of an arbitrary substitution weight matrices, etc.
(1) S(1) = 182; D(1) = 41
1 ! VLSAADKTNVKAAWSKVGGHAGEYGAEALERMFLGFPTTKTYFPHF
1 ! VqlsgeekaavlAlwdkvneeevgGealgrllvvypwTqrffdsfg
|=======================>
47 ! DLSHGSAQ_____VKAHGKKVGDALTLAVGHLDDLPGA
47 ! DLSnpgAvmgnpkVKAHGKKVlhsfgegVhHLDnLkGt
============================================================
(2) S(2) = 223; D(2) = 49
<=======================
1 ! VLSAADKTNVKAAWSKVGGHAGEYGAEALERMFLGFPTTKTYFPHF
1 ! VqlsgeekaavlAlwdkvnee_EvGgEALgRllvvyPwTqrfFdsF
=======|
47 ! DLSHGSAQ_______VKHGKKVGDALTLAVGHLDDLPGA
46 ! gdlsnpgaVmgnpkvkAHGKKVlhsfgegVhHLDnLkGt
============================================================
(3) S(3) = 272; D(3) = 31
|=================>
1 ! V_LSAADKTNVKAAWSKVGGHAGEYGAEALERMFLGFPTTKTYFPHF
1 ! VqLSgeeKaaVlAlWdKVnee__EvGgEALgRllvvyPwTqrfFdsF
47 ! DLSHGSAQ______VKAHGKKVGDALTLAVGHLDDLPGA
46 ! gdlsnpgaVmgnpkvkAHGKKVlhsfgegVhHLDnLkGt
============================================================
(4) S(4) = 303; D(4) = 7
1 ! V_LSAADKTNVKAAWSKVGGHAGEYGAEALERMFLGFPTTKTYFPHF_
1 ! VqLSgeeKaaVlAlWdKVnee__EvGgEALgRllvvyPwTqrfFdsFg
|======>
47 ! DLSHGSAQ_____VKAHGKKVGDALTLAVGHLDDLPGA
47 ! DLSnpgAvmgnpkVKAHGKKVlhsfgegVhHLDnLkGt
============================================================
(5) S(5) = 310; D(5) = 10
1 ! V_LSAADKTNVKAAWSKVGGHAGEYGAEALERMFLGFPTTKTYFPHF_
1 ! VqLSgeeKaaVlAlWdKVnee__EvGgEALgRllvvyPwTqrfFdsFg
|==>
47 ! DLSH_GSAQ____VKAHGKKVGDALTLAVGHLDDLPGA
47 ! DLSnpGavmgnpkVKAHGKKVlhsfgegVhHLDnLkGt
============================================================
(6) S(6) = 320; D(6) = 7
1 ! V_LSAADKTNVKAAWSKVGGHAGEYGAEALERMFLGFPTTKTYFPHF_
1 ! VqLSgeeKaaVlAlWdKVnee__EvGgEALgRllvvyPwTqrfFdsFg
<=|
47 ! DLSHGSAQ_____VKAHGKKV____GDALTLAVGHLDDLPGA
47 ! DLSnpgAvmgnpkVKAHGKKVlhsfGeg____VhHLDnLkGt
Figure 2. The maximal alignments of the alpha- vs beta-chain of horse hemoglobin (PDB code 2mhb) containing 1, 2, 3, 4, 5 and 6 gaps respectively (cf. Fig. 2) and providing (for each g) the maximal possible total weight of substitutions S(g). The ends of alignments containing no gaps are omitted.The arrows |===> and <====| mark regions which are shifted with respect to previous alignment. Note that a length of these fragments decrease with g. The alignment with 4 gaps is the critical one, it coincides with the alignment shown in the 3D-ALI database.
S. 0.3 0.4 0.5 0.6 0.7 0.8 0.9
L
200 7.3 5.8 4.1 3.1 2.7 1.1 1.0
300 7.3 5.9 4.15 3.5 3.1 1.6 1.0
700 7.8 6.1 4.25 3.6 2.7 1.75 1.0
1000 8.05 6.1 4.35 3.25 2.9 2.0 1.45
Figure 3. The average values of the possiible jumps D(g) obtained for the random nucleotide sequences with the different rates of similarity (S) and different lengthes (L). For each S = 0.3, 0.4, …, 0.9 and for each L = 200, 300, 700, 1000 we have performed a series of alignments. For the given L and S one of the sequences aligned is a random nucleotide sequence oflength L, and the other sequence is obtained from the first one by random substitutions in L (1-S) random positions (cf. the case S1 above).
Acknowledgements
The authors are greatful to A.V.Finkelstein, M.S.Gelfand, S.R.Sunyaev, P.Pevzner and M.S.Waterman for fruitful discussions.
References
- Altschul S. (1993) “A protein alignment scoring system sensitive at all evolutionary distances”, Mol. Evol., v.36, p.p. 290-300
- Aho A., Hopcroft J. and Ullman J.(1976) “The Design and Analysis of Computer Algorithms”. Addison-Wesley..Reading, MA
- Finkelstein A.V. and Roytberg M.A. (1993) “Computation of biopolymers: A general approach to different problems”. BioSystems, v. 30, pp 1-20.
- Gusfield D., Balasubramian K. and Naor K. (1994). “Parametric Optimization of Sequence alignment.” Algorithmica,v.12, pp. 312-326
- Pascarella, S. and Argos, P. (1992) Prot. Engng., v. 5, pp. 121-137
- Roytberg M.A. (1994) “Pareto-optimal alignments of symbol sequences”, Preprint, Pushchino
- Thompson, J.D., Higgins, D.G. and Gibson, T.J. (1994) “Improved sensitivity of profile searches through the use of sequence weights and gap excision.” CABIOS, 10, 19-29
- Vingron, M. and Sibbald, P.R. (1993) “Weighting in sequence space: a comparison of methods in terms of generalized sequences”. Proc. Natl. Acad. Sci. USA, 90, 8777-8781
- Vingron M. and Waterman M.S. (1994) ” Sequence alignment and penalty choice: Review of concepts, case studies and implications.”. J. Mol.Biol., v. 235, pp. 1 – 12.
- Waterman M.S. (1995) “Introduction to computational biology”, Chapman&Hall Press, UK
- Waterman M.S., Eggert, M and Lander, E (1992). “Parametric sequence comparisons.” Proc. Nat. Acad. Sci. U.S.A. v.89, 6090-6093.
