LATENT PERIODICITY OF PROTEIN SEQUENCES

KOROTKOV E.V.+, KOROTKOVA M.A.1

Center “Bioengineering”, Russian Academy of Sciences, Prospect 60-tya Oktyabrya, 7/1, 117322, Moscow, Russia;
e-mail: korotkov@biengi.msk.su;

1Department of Cybernetics, Moscow Physical Engineering Institute, Kashirskoe shosse 31, 115409, Moscow, Russia;

+Corresponding author

Keywords: protein sequence, periodicity, mutual information, Monte Carlo, sequence similarity

Introduction

The study of protein sequence periodicity is one of the numerous approaches to protein structure investigations. The purpose of these investigations is to find structural peculiarities of amino acid sequences and their relations with a spatial organization of proteins. Two mathematical approaches are widely used for this purpose now. The first method is the classical Fourier transformation of a symbolic sequence (1,2,3). The fundamental difficulties with Fourier analyses or autocorrelation techniques for symbolic sequences are a manner of transformation to numerical sequence (or sequences) saving all statistical properties of a symbolic sequence and impossibility to find periodicity in sequence with deletions and insertions.

The second method is algorithmic investigations of symbolic sequences. The approaches to the search of tandem repeats by this method were developed earlier (4,5,6,7). These algorithmic methods are usually based on the dynamic programming of the alignment of pair sequences (8). Developed methods permit to find an amino acid sequence periodicity with mutations, deletions and insertions.

The number of mutations between any two periods, where the periodicity can be revealed, should not be very high. If the periods have not got any visible homology, then using Fourier transformation and algorithmic approaches it is not possible to find sequence periodicity. In Fourier analysis the homology search is introduced in the manner of transformation of a symbolic sequence to a numerical sequence. In the dynamic programming it is determined using of the PAM-250 (or similar matrixes) calculated for the comparison of closely related proteins.

We can consider the situation when periodicity is a common feature of all periods. This periodicity (we call this periodicity latent) is different from the homology type (when we can find the similarity between periods). We can find it if we analyze all periods. For example, the existence of the following period in the sequence is possible: {(Lys\Asn\Ile\Met\Thr)(Arg\Ser\Pro\Hys\Glu) (Gln\Val\Ala\Asp\Gly)}. The first position of the period has one erosion type of amino acids, the second position of the period has another erosion type of amino acids. The third position has the erosion type of amino acids, that differs from the erosion type of the first and second positions. If the sequence has enough length, then the latent periodicity can be found as statistically important. We can find this periodicity in the sequence: [LysArgGln][AsnSerVal][IleProAlaMet][HysAspThr][GluGlyLys][HysAspGly]… The brackets show the periods. The statistically important homology between any two periods of this sequence is absent or very low but the periodicity is present in the sequence. We can produce many types of a latent periodicity for given length of a period. The number of types is increased with grow of a period length.

The reasons for latent periodicity creation in protein sequences can be different. It is possible to assume that a periodicity in protein spatial organization can influence amino acid sequences. The alternation of -structures and  -helices can create a latent periodicity of amino acid sequences. Very ancient tandem duplications in amino acid sequence can create a latent periodicity also.

Methods and Algorithms

To find the latent periodicity of amino acid sequences we should develop a new mathematical method. In present report we modify the suitable mathematical method that we elaborated earlier for DNA sequence analysis (9,10,11). The method uses the principle of enlarged similarity between symbolic sequences (12). For the search of the protein latent periodicity we compared an artificial periodical symbolic sequence with a protein sequence to be analyzed. The sequence S(1)S(2)…S(n)S(1)S(2)…S(n)S(1)S(2)…S(n)… is created for finding periods with the length equal to n. The length of the artificial sequence is equal to the length of the analyzed protein sequence. The artificial sequences with periods from 2 to L/2 are compared with protein sequence in question one after another. L is the length of investigated protein sequence. Matrix M(20,n) is filled for each comparison. M(i,j) element shows the number of i type amino acids that are situated opposite the letter S(j) of the artificial sequence. The measure of similarity between two compared sequences is selected as mutual information, calculated from matrix M(20,n). We analyzed relatively short amino acid sequence and used method Monte-Carlo for the estimation of the statistical importance of the mutual information. It is suitable to take value Z=(I(1)-I'(average))/ as quantitative measure of the statistical importance of a periodicity in an amino acid sequence. Here Ií(average) is an average value of mutual information Ií for lot of random Mí matrixes with the same marginal frequencies as M(20,n) matrix, D is the dispersion of Ií. If Z is low or equals to zero than the similarity between artificial and protein sequences is absent and the protein sequence has not got any periodicity. The Z value has an approximately normal distribution. We selected protein sequences with Z>5.8. It gives the probability of random relationship between artificial periodical and amino acid sequences less than 10-8.

As a result of calculations we have the spectrum of Z for different n. This spectrum shows a presence of different amino acid periods in analyzed protein sequences. Z(n) spectrum is possible to determine for period length at equal to L/2. It gives the chance to find not only the latent protein periodicity but also all duplications in a protein sequence.

Latent periodicity can occupy a part of a known amino acid sequence from the data bank. To find an amino acid region with most expressed latent periodicity we should test all positions of the left and right borders and we can calculate the Z(n) spectrum for each positions of the borders. The time for analysis of the periodicity of one sequence with the length equals to 500 amino acids was about 3 minutes if we used Pentium 200 processor.

Results and Discussion

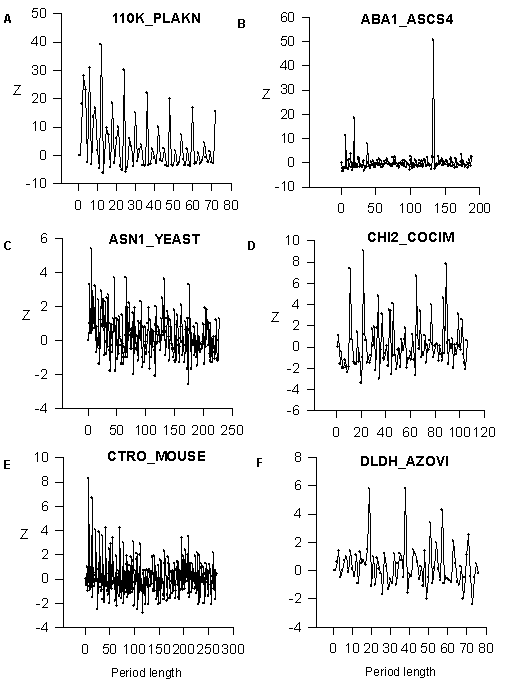
We analyzed the SWISS-PROT data bank and found that more 15% of known proteins have the regions with a latent periodicity (5.8<Z<7.0). We found the big number of perfect periodicity cases and tandem duplications. These cases are revealed for Z>7.0 Firstly, we show the dependence Z(n) for amino acid sequences with perfect periodicity. It illustrates the power of developed mathematical method (Fig.1). The first sequence is a part of 110K_PLAKN clone from SWISSPROT; the sequence contains 12 direct tandem repeats ETQNTVEPEQTE. It is possible to see from Fig.1A that Z has maximum for n=12 and it is equal to 44. The probability P for random occurrence of such periodicity can be estimated as less that 10 -100 using the formula: P=(e-Z1)/(Z), where Z1= Z2 and P is the probability (Feller, 1970). For n=24, 36, 48… Z is equal to 24.5, 26.6 and 17.1 correspondingly and for n=3, 4, 6, 8 and 9 we have Z equals to 28, 26.5, 31, 15 and 15,8. The period equals to 12 amino acids influences these periods and gives big values of Z. But Z(12) is the maximum value of Z for all periods. The second example of the perfect periodicity is shown in Fig.1B. Amino acid sequence from ABA1_ASCS4 clone of SWISSPROT data bank tandem repeats AKILHYYDELEGDAKKEATEHLKGGCREIL KHVVGEEKAAELKNLKDSGASKEELKAKVEEALHAVTDEEKKQYIADFGPACKKIYGVHTSRRRRHHFTLESSLDTHLKWLSQEQKDELLKMKKDGKAKKELE. The length of period is equal to 133 amino acids and Z(133)=50.6. The period that is equal to 133 amino acids gives the Z(7)=11,3, Z(19)=18.5 and Z(38)=8.0. But it is possible to see that the period equals to 133 amino acids has the maximum value of Z.

In Fig.1(C-F) we show as example the latent periodicity of the next proteins. Glutamine-dependent asparagine synthetase from ASN1_YEAST clone endochitinase 2 of CHI2_COCIM clone; citron protein from CTRO-MOUSE clone; lipoamide dehydrogenase of Azotobacter vinelandii from DLDH_AZOVI clone. These protein sequences have lengths of the latent periods that are equal to 6, 11, 7 and 19 amino acids correspondingly. The region with latent periodicity in DLDH_AZOVI clone includes the NAD+-binding site of the lipoamide dehydrogenase (13). NAD+-binding site is a very conservative sequence that occurs in many proteins. The region containing NAD+-binding site, includes 4 a -helices and 6 b -structures, but variations in the number of structure elements is possible.

Figure 1 The Z values for the sequences with perfect periodicity from 110K_PLAKN and ABA1_ASCSU and for sequences with latent periodicity from ASN1_YEAST clone, CHI2_COCIM clone, CTRO-MOUSE clone and DLDH_AZOVI clone. The abscissa axis shows the period length in amino acids.

The precise structure of NAD+-binding site includes 32 amino acids and contains -fold (14). 11 rules describe the type of amino acid that should occur at specific position in this peptide fragment (14). The rules differ from the matrix shown in Fig.4 for DLDH_AZOVI clone. 19 amino acid repeat, found in this study, includes the -fold of NAD+-binding site. The primary sequence forduplication can includes one  -structure and one a -helix. The duplications of this primary sequence could create the region, containing the NAD+-binding site.

The significance of a found periodicity may be different, in some cases latent periodicity can relate to the laws of a protein spatial organization. We can assume that several alternating of   -folds and some other protein structures require latent periodicity of amino acids sequences. Periods can be considered as elementary “bricks” of certain protein structures. Latent periodicity of coding DNA sequences can reflect the evolution of proteins by means of duplications of initial relatively short DNA sequence for creation of variant of protein structures. The data banks of the DNA and protein sequences with latent periodicity are developed now.

References

  1. A.D.McLachlan “Multichannel fourier analysis of patterns in protein sequences” J.Phys.Chem. 97,3000 (1993)
  2. V.Ju.Makeev V.G.Tumanyan “Search of periodicities in primary structure of biopolymers: a general Fourier approach” Comput. Appl. Biosci. 12,49 (1995)
  3. V.R. Chechetkin, A.Yu.Turygin ëíSearch of hidden periodicities in DNA sequencesíí J.Theor.Biol. 175,477 (1995)
  4. J.Heringa, P.Argos “A method to recognize distant repeats in protein sequences” Proteins. 17,341 (1993)
  5. G.Benson S.Waterman “A method for database search for all k-nucleotide repeats” Nucl.Acid Res. 22,4828 (1994)
  6. G.Benson “Sequence alignment with tandem duplications” J.Comput. Biol. 4, 351 (1997)
  7. J.Heringa “The evolution and recognition of protein sequence repeats” Comput.Chem. 18,233 (1994)
  8. S.B.Needleman C.D.Wunch “A general method applicable to search for similaritites in the amino acids sequences of two proteins” J.Mol.Biol., 48, 443 (1970)
  9. E.V.Korotkov, M.A.Korotkova “DNA regions with latent periodicity in some human clones” DNA Sequence. 5, 353 (1995)
  10. E.V.Korotkov, D.A.Phoenix “Latent periodicity of DNA sequences of many genes” In: Proceedings of Pacific Symposium on Biocomputing 97. Maui, Hawaii, USA: Word Scientific Press. p.222 (1997)
  11. E.V.Korotkov, M.A.Korotkova, J.S.Tulko “Latent sequence periodicity of some oncogenes and DNA-binding protein genes” Comput. Appl. Biosci. 13, 37 (1997)
  12. E.V.Korotkov, M.A.Korotkova “Enlarged similarity of nucleic acids sequences” DNA Research 3, 157 (1996)
  13. A.H.Westphal, A.de Kok “Lipoamide dehydrogenase from Azotobacter vinelandii: Molecular cloning, organization and sequence analysis of the gene” Eur. J. Biochem. 72, 299 (1986)
  14. R.K.Wierenga, P.Terpstra, W.G.J.Hol “Prediction of the occurence of the ADP-binding    -fold in proteins, using an amino acid sequence fingerprint” J.Mol.Biol. 187, 101 (1986)