AULCHENKO Yu.S.+, AXENOVICH T.I.
Institute of Cytology and Genetics, Siberian Branch of the Russian Academy of Sciences, 10 Lavrentiev Ave., Novosibirsk, 630090, Russia;
e-mail:yurii@bionet.nsc.ru
+Corresponding author
Keywords: pedigree data, linkage analysis, peeling technique
1. Introduction
The method of maximum likelihood is widely used in segregation and linkage analysis of pedigree data. There are efficient algorithms to compute the likelihood for a pedigree without loops [1,2]. In human pedigrees without or with a few loops are common, so these algorithms are suitable and highly effective for data analysis. The situation in livestock and laboratory pedigrees is quite different: such pedigrees contain multiple loops as a rule. Although general algorithms to compute the likelihood for a pedigree with loops have been also developed [3-5], their application meets a serious difficulties in pedigrees with multiple loops, because it demands unbelievable computing resources.
The methods of approximate likelihood calculation look rather promising for computing the likelihood for large complex pedigrees with multiple loops. Recently, Monte Carlo procedures have been applied for a set of problems of segregation and linkage analysis [6-7]. However, the method is critically dependent on some assumption that do not always hold [8]. Another access to the likelihood calculation for a pedigree with loops is simplification of pedigree’s structure, i.e. cutting loops [9]. Cutting all loops result in a zero-loop pedigree; then the likelihood for the pedigree might be calculated by common efficient methods widely used in the analysis of human pedigrees. It have been shown that the approximation of the likelihood by cutting might be improved by a set of strategies [10].
The main advantage of approximation of a likelihood by cutting is its efficiency in the sense of small storage and computing time requirements. However, the question of its efficiency in the sense of dependence of the results obtained with the method on the nature of a trait and on the pedigree structure needs thorough investigation.
2. Theoretical background
Here we consider the efficiency of different approximations of the likelihood by cutting with respect to the accuracy of hypotheses testing, estimating type I error in the Elston-Stewart test for major gene [1].
Cutting loops should lead to decreased amount of genetic information available. First, the more loops should be cut, the more information should be lost. Second, in general, the shorter a loop to be cut, the more information lost. The consequence of the loss of information should be decreased accuracy of parameter estimates and hypotheses testing.
From the set of strategies to improve the likelihood approximation by cutting the extra-extension/conditioning [10] seems to be the most valuable. The extra-extension allows further qualification of the genotype of cut individual, thus improving the likelihood approximation. This approach gives excellent results (i.e. exact likelihood) if it is possible to reconstruct the genotype of an individual to be cut. However, the very wide range of situations do not allow for exact knowledge of a genotype.
The variety of short loops is comparatively small. This fact allows constructing efficient peeling algorithm for calculation the likelihood for pedigrees with short loops. This approach should be a priori better then any approximation, because it allows calculate exact likelihood for short loops. It should be noted that the number of calculations and storage space required for exact processing of short loops might be even less then that required by the algorithm of cut-extension/conditioning. Another side of this approach is that it is restricted to the case of very short loops, because variety of loops is exponential on the length. In this case the extra-extension/conditioning seems to be a valuable tool for improvement of likelihood approximation by cutting.
Here we concentrate on the damage which may appear because of cutting short loops and therefore we consider real livestock pedigree containing multiple backcrosses and long loops. The distribution of mendelian binary trait on the pedigree was simulated, then genetic parameters were estimated and segregation analysis was performed using three different approaches to approximate the likelihood for a pedigree with loops. Two of three are these presented by Stricker et al. [9] and Wang et al. [10], the latter one was developed by us and involve the procedure which allow for peeling close inbred loops and thus approximate the likelihood by cutting only long loops [12].
3. Calculation of the likelihood by peeling
The likelihood calculation was performed using modified computer program MAN-A1 [11]. The program allows calculation of the likelihood for a pedigree without loops. It uses peeling technique to derive the likelihood at specified values of parameters.
The basic idea of peeling is collapsing information from a part of a pedigree onto other part. For example, genotypes of a nuclear family members are conditionally independent of the genotypes of other pedigree members given connectors’ genotypes. This means that any nuclear family which contains only one member who mates outside of the nuclear family (connector) might be peeled onto this single connector. Efficient peeling algorithm of likelihood calculation for a pedigree without loops is based on successive peeling of nuclear families onto connectors, the process which results in collapsing all pedigree information onto one of the pedigree’s members.
Two basic peelings are necessary for calculation of the likelihood for a pedigree without loops. First, peeling of a nuclear pedigree onto one of the parents and second, peeling of a nuclear pedigree onto one of the offspring. These peelings are sufficient for the approximate likelihood calculation if all loops are cut. However, as we have mentioned above, cutting close loops could be avoided. The improvement of likelihood approximation by cutting was obtained by insertion of additional procedure for peeling short inbred loops [12]. Thus approximation of the likelihood was achieved by cutting only long loops. We retained intact the main idea of peeling a pedigree without loops: to peel a pedigree structure onto single connector. This allowed easy introduction of a new peeling in computer program MAN-A1 (as well as it is easy to introduce the peeling into any program which use peeling technique) and did not decrease efficiency. The procedure which we introduced allows peeling the nuclear pedigree with close inbred crosses (backcrosses or/and brother-sister crosses) associated with it onto one of the parents in the nuclear pedigree.
4. Comparison of the methods
4.1. Material: pedigree and simulated data
In this analysis we used a pedigree of pigs experimental farm of the Institute of Cytology and Genetics SD RAS. The pedigree contains 568 individuals mating in 60 crosses. Its structure is rather complex: there are many long loops and short inbred ones, such as backcross-loops. Many individuals are involved in multiple mating, for example one of the males mates 24 times. Only three nuclear pedigrees could be peeled by basic peelings. Monte-Carlo methods were used to simulate binary data on the pedigree. The data were generated under the model of autosomal diallelic inheritance assuming of Hardy-Weinberg equilibrium. Model parameters were: the population frequency of a allele was equal to q=0.5, the probabilities of phenotypes’ expression given genotype were equal to w(AA)=0.0, w(Aa)=0.5 and w(aa)=1.0. The distribution of the trait in the pedigree was simulated in 500 samples.
4.2. Methods under comparison
The approaches to approximate the likelihood we studied were: (1) conditional approximation of the likelihood by cutting as it was described in the papers [9] and [10]. Loops were cut by introducing artificial founders with the same phenotype as original individual had. This approach resulted in cut-extended loop-less pedigree with 608 members. Conditioning mean that after calculation of the likelihood for cut-extended pedigree it was divided by the likelihood of extended part. The likelihood of extended part was calculated as a likelihood of the cut-extended pedigree after setting the phenotypes of original individuals to be missed. (2) Conditional approximation with extra-extension [10]. Loops were cut by introducing artificial nuclear pedigrees if an individual to be cut had parents in the pedigree or by introducing artificial founder if an individual to be cut was founder. This resulted in cut-extended pedigree with 754 members mating in 74 crosses, of which additional 14 emerged in the process of extra-extension.
Methods (1) and (2) assume cutting all loops in the pedigree and implementation of basic peelings to calculate the likelihood. The method (3) involves the additional procedure for peeling close inbred loops [12]: (3) conditional approximation by cutting only long loops. Loops were cut by introducing artificial founders. This approach resulted in cut-extended pedigree with multiple short inbred loops containing 587 members.
The results obtained with exact likelihood should be considered as the “gold standard” to compare approximations with. We calculated exact likelihood using the algorithm of “creation of genotypic copies” [3-4]; this algorithm is time-consuming because creation of genotypic copies of k individuals increases time of likelihood computation approximately in |G|k times (|G| denotes the number of possible genotypes).
4.3. Characteristics for comparison
We characterized different approaches to approximate the likelihood with the respect to the following features: 1) standard deviation of the mean maximum likelihood estimate (MLE) of a genetic parameter and 2) the frequency of false rejection of mendelian inheritance. To evaluate hypotheses, the likelihood ratio test was used by taking the twice the negative difference between the loge likelihoods of not restricted and mendelian transmission probabilities hypotheses. On the common number of degrees of freedom in this test should be three in the case of three transmission probabilities. However, in the process of estimation some of the estimates of transmission probabilities may converge to bounds. In this case the number of degrees of freedom should be less then three, but no less three minus the number of transmission probabilities estimated at the bound. We estimated the lower and upper frequency of false rejection by setting number of degrees of freedom to three and DFmin which was calculated for each particular case.
4.4. Comparison results
The mean of parameter estimates obtained with different methods did not differ too much from the parameters of the model. The fig. 1 graphically represents magnitude of the standard deviations adjusted to the standard deviation of the MLE derived with the exact method. It can be seen that results obtained by cutting all loops by introducing only artificial founders/conditioning (1) and by extra-extension/conditioning (2) are nearly the same and are of about 1.5 times greater then SD(MLE) obtained using exact method; cutting only long loops rather then all (3) decreases standard deviation nearly to the value obtained with exact method.
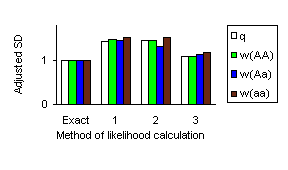
Figure 1. Standard deviation of MLE derived by different approaches to calculate the likelihood adjusted on the SD(MLE) obtained by maximizing exact likelihood.
The accuracy of parameter estimates is in direct relation with the accuracy of hypotheses testing, but it is not so illustrative as a frequency of false rejections of true hypothesis (type I error). The frequency of false rejection of mendelian inheritance is presented in the Fig. 2. White columns represent the lower (DF=3) and the black ones the upper (DFmin) frequency of false rejection of mendelian inheritance.
The frequency of false rejection of mendelian segregation for exact method is at most 0.05. In the case of approximation likelihood by cutting/conditioning (1) the frequency of false rejection of mendelian inheritance is equal to 0.07 and 0.16 for different number of degrees of freedom. Extra extension (2) improve this a little, but the frequency of false rejection still do exceed 0.05. Approximation of the likelihood by cutting only long loops and conditioning (3) decrease the frequency of false inferences down to the level of 0.03 and 0.06, respectively, which is close to that of exact method. Thus, the false rejection of mendelian inheritance is mainly due to cutting short inbred loops.

Figure 2. The frequency of false rejection of mendelian inheritance under different approaches to calculate the likelihood.
Our results lead to conclusions that cutting short inbred loops may lead to dramatic increase in the frequency of false inferences. This could be easily avoided by using special peeling. Another conclusion that could be made is that extra-extension in the case of cutting long loops might be unnecessary because even conditioning gives good results. However, from the analysis we cannot inference on what is the damage from cutting loops of intermediate size.
In general, the approach which unify cut/extra-extension/conditioning long and intermediate loops with peeling short loops seems to be a reasonable tool for analysis of large livestock/laboratory pedigrees with multiple loops.
Acknowledgements
This research was partly supported by the grants from Russian Foundation for Basic Research
96-15-97738 and International Soros Science Education Program a98-20 (A.Yu.S.)
References
- C. Elston and J. Stewart, “A general model for the genetic analysis of pedigree data”, Hum Hered. 21, 523 (1971)
- C. Elston, “Segregation analysis”, Adv.Hum Genet 11, 63 (1981)
- K. Lange and R. C. Elston, “Extensions to pedigree analysis I. Likehood calculations for simple and complex pedigrees”, Hum. Hered. 25, 95 (1975)
- J. Ott, “A computer program for linkage analysis of general human pedigrees”, Am. J. Hum. Genet. 28, 528 (1976)
- C. Cannings, E. A. Thompson and M. H. Skolnick, “Probability function on complex pedigrees”, Adv. Appl. Prob. 10, 26 (1978)
- Thompson and S.-W. Guo, “Evaluation of likelihood ratios for complex genetic models”, IMA J Math. Appl. Med. Biol. 8, 149 (1991)
- K. Lange and E. Sobel, “A random walk method for computing genetic location scores”, Am. J. Hum. Genet. 49, 1320 (1991)
- K. Lange and S. Matthysse, “Simulation of pedigree genotypes by random walks”, Am. J. Hum. Genet. 58, 1323 (1989)
- Stricker, R. L. Fernando and R. C. Elston, “An algorithm to approximate the likelihood for pedigree data with loops by cutting”, Theor. Appl. Genet. 91, 1054 (1995)
- T. Wang, R. L. Fernando, C. Stricker and R. C. Elston, “An approximation to the likelihood for a pedigree with loops”, Theor. Appl. Genet. 93, 1299 (1996)
- T.I. Axenovich and E.Kh. Ginzburg, “A system for mendelian analysis of alternative traits MAH-A1”, Genetika 23, 268 (1987)
- Yu.S. Aulchenko and T.I. Axenovich, “Calculation of the likelihood for pedigrees with close inbred loops”, (submitted)
